题目内容
5.曲线$y={(\frac{1}{3})^x}$与$y={x^{\frac{1}{2}}}$的交点横坐标所在区间为( )| A. | $(0,\;\frac{1}{3})$ | B. | $(\frac{1}{3},\;\frac{1}{2})$ | C. | $(\frac{1}{2},\;\frac{2}{3})$ | D. | $(\frac{2}{3},\;1)$ |
分析 方法一:分别画出$y={(\frac{1}{3})^x}$与$y={x^{\frac{1}{2}}}$的图象,由图象,结合各选项即可判断.
方法二:构造函数,利用函数零点存在定理,即可判断
解答 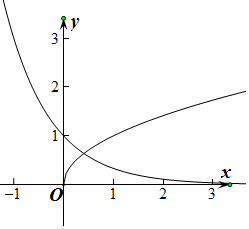 解:方法一:分别画出$y={(\frac{1}{3})^x}$与$y={x^{\frac{1}{2}}}$的图象,如图所示,
解:方法一:分别画出$y={(\frac{1}{3})^x}$与$y={x^{\frac{1}{2}}}$的图象,如图所示,
由图象可得交点横坐标所在区间为($\frac{1}{3}$,$\frac{1}{2}$),
方法二:设f(x)=($\frac{1}{3}$)x-x${\;}^{\frac{1}{2}}$,
∵f($\frac{1}{3}$)=($\frac{1}{3}$)${\;}^{\frac{1}{3}}$-$(\frac{1}{3})^{\frac{1}{2}}$<0,
f($\frac{1}{2}$)=($\frac{1}{3}$)${\;}^{\frac{1}{2}}$-($\frac{1}{2}$)${\;}^{\frac{1}{2}}$>0,
∴f($\frac{1}{3}$)f($\frac{1}{2}$)<0,
根据函数零点存在定理可得点函数零点所在区间为($\frac{1}{3}$,$\frac{1}{2}$),
即交点横坐标所在区间为($\frac{1}{3}$,$\frac{1}{2}$),
故选:B
点评 本题考查了函数图象的识别和画法和函数零点存在定理,属于基础题.

练习册系列答案
相关题目
10.设复数z满足z(1+i)=i(i为虚数单位),则|z|=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
14.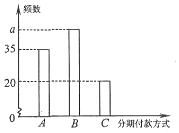 某知名品牌汽车深受消费者喜爱,但价格昂贵.某汽车经销商推出A,B,C三种分期付款方式销售该品牌汽车,并对近期100位采用上述分期付款的客户进行统计分析,得到如下的柱状图.已知从A,B,C三种分期付款销售中,该经销商每销售此品牌汽车1辆所获得的利润分别是1万元,2万元,3万元.以这100 位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率.
某知名品牌汽车深受消费者喜爱,但价格昂贵.某汽车经销商推出A,B,C三种分期付款方式销售该品牌汽车,并对近期100位采用上述分期付款的客户进行统计分析,得到如下的柱状图.已知从A,B,C三种分期付款销售中,该经销商每销售此品牌汽车1辆所获得的利润分别是1万元,2万元,3万元.以这100 位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率.
(Ⅰ)求采用上述分期付款方式销售此品牌汽车1辆,该汽车经销商从中所获得的利润不大于2万元的概率;
(Ⅱ)求采用上述分期付款方式销售此品牌汽车1辆,该汽车经销商从中所获得的利润的平均值;
(Ⅲ)根据某税收规定,该汽车经销商每月(按30天计)上交税收的标准如表:
若该经销商按上述分期付款方式每天平均销售此品牌汽车3辆,估计其月纯收入(纯收入=总利润-上交税款)的平均值.
 某知名品牌汽车深受消费者喜爱,但价格昂贵.某汽车经销商推出A,B,C三种分期付款方式销售该品牌汽车,并对近期100位采用上述分期付款的客户进行统计分析,得到如下的柱状图.已知从A,B,C三种分期付款销售中,该经销商每销售此品牌汽车1辆所获得的利润分别是1万元,2万元,3万元.以这100 位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率.
某知名品牌汽车深受消费者喜爱,但价格昂贵.某汽车经销商推出A,B,C三种分期付款方式销售该品牌汽车,并对近期100位采用上述分期付款的客户进行统计分析,得到如下的柱状图.已知从A,B,C三种分期付款销售中,该经销商每销售此品牌汽车1辆所获得的利润分别是1万元,2万元,3万元.以这100 位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率.(Ⅰ)求采用上述分期付款方式销售此品牌汽车1辆,该汽车经销商从中所获得的利润不大于2万元的概率;
(Ⅱ)求采用上述分期付款方式销售此品牌汽车1辆,该汽车经销商从中所获得的利润的平均值;
(Ⅲ)根据某税收规定,该汽车经销商每月(按30天计)上交税收的标准如表:
| 月利润(单位:万元) | 在(0,100]内的部分 | 超过100且不超过150的部分 | 超过150的部分 |
| 税率 | 1% | 2% | 4% |