题目内容
15.已知点(x,y)满足约束条件$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+y≤2a}\\{x-y≤a}\end{array}\right.$(其中a为正实数),则z=2x-y的最大值为4.分析 画出约束条件的可行域,利用目标函数的几何意义求解即可.
解答 解:点(x,y)满足约束条件$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+y≤2a}\\{x-y≤a}\end{array}\right.$(其中a为正实数),可行域如图:目标函数的z=2x-y在B处取得最大值,由$\left\{\begin{array}{l}{x+y-2a=0}\\{x-y-a=0}\end{array}\right.$可得B($\frac{3a}{2}$,$\frac{a}{2}$).
所以z的最大值为:2×$\frac{3a}{2}-\frac{a}{2}$=10,解得a=4.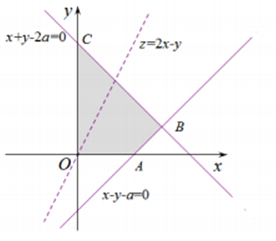
故答案为:4.
点评 本题考查线性规划的应用,意在考查数形结合思想的灵活应用,考查计算能力.

练习册系列答案
相关题目
6.用三段论推理:“任何实数的绝对值大于0,因为a是实数,所以a的绝对值大于0”,你认为这个推理( )
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 是正确的 |
3.若直线mx+2y+m=0与直线3mx+(m-1)y+7=0平行,则m的值为( )
| A. | 7 | B. | 0或7 | C. | 0 | D. | 4 |
10.设复数z满足z(1+i)=i(i为虚数单位),则|z|=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
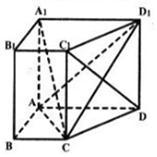 如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD是直角梯形,其中
如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD是直角梯形,其中