题目内容
20.已知圆M:(x+1)2+y2=1圆N:(x-1)2+y2=9,动圆P与圆M外切并与圆N内切,圆心P的轨迹为曲线C.(1)求C的方程;
(2)若过点(1,0)的直线与曲线C交于R,S两点,问是否在x轴上存在一点T,使得当k变动时总有∠OTS=∠OTR?若存在,请说明理由.
分析 (1)确定PF1|+|PF2|=4>|F1F2|,可得曲线E是长轴长2a=4,焦距2c=2的椭圆,且b2=a2-c2=3,即可求E的方程;
(2)假设存在T(t,0)满足∠OTS=∠OTR.联立得(3+4k2)x2-8k2x+4k2-12=0,由此利用根的判别式、韦达定理,结合已知条件能求出存在T(4,0),使得当k变化时,总有∠OTS=∠OTR.
解答 解:(1)设动圆P的半径为r,由已知|PF1|=r+1,|PF2|=3-r,
则有|PF1|+|PF2|=4,
由椭圆的定义可知,曲线C是以M,N为左右焦点,长半轴长为2,短半轴为$\sqrt{3}$的椭圆(左顶点除外),其方程为$\frac{x^2}{4}+\frac{y^2}{3}=1({x≠-2})$.…(5分)
(2)假设存在T(t,0)满足∠OTS=∠OTR.设R(x1,y1),S(x2,y2)
联立$\left\{\begin{array}{l}y=k({x-1})\\ 3{x^2}+4{y^2}-12=0\end{array}\right.$得(3+4k2)x2-8k2x+4k2-12=0,
由韦达定理有x1+x2=$\frac{8{k}^{2}}{3+4{k}^{2}}$,x1x2=$\frac{4{k}^{2}-12}{3+4{k}^{2}}$①,其中△>0恒成立,…(7分)
由∠OTS=∠OTR(显然TS,TR的斜率存在),故kTS+kTR=0即$\frac{{y}_{1}}{{x}_{1}-t}+\frac{{y}_{2}}{{x}_{2}-t}$=0②,
由R,S两点在直线y=k(x-1)上,故 y1=k(x1-1),y2=k(x2-1),
代入②整理有2x1x2-(t+1)(x1+x2)+2t=0③…(9分)
将①代入③即有:$\frac{6t-24}{3+4{k}^{2}}$=0④,要使得④与k的取值无关,当且仅当“t=4“时成立,
综上所述存在T(4,0),使得当k变化时,总有∠OTS=∠OTR.…(12分)
点评 本题考查椭圆的定义与方程,考查直线与椭圆的位置关系,考查直线过定点,属于中档题.

| A. | $\frac{3}{2}$或$\frac{2}{3}$ | B. | $\frac{4}{3}$或$\frac{3}{4}$ | C. | $\frac{5}{3}或\frac{3}{5}$ | D. | $\frac{5}{4}或\frac{4}{5}$ |
| A. | 相切 | B. | 相离 | ||
| C. | 相交且直线过圆心 | D. | 相交且直线不过圆心 |
| A. | 内心 | B. | 外心 | C. | 重心 | D. | 垂心 |
| A. | y=2x-1.5 | B. | y=0.8x+3.3 | C. | y=-2x+14.5 | D. | y=-0.6x+9.1 |

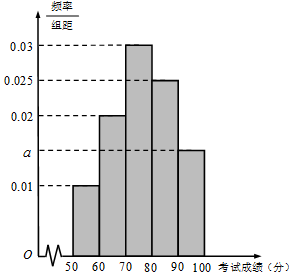 某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据进行分组,分组区间为:[50,60),[60,70),[70,80),[80,90),[90,100],并绘制出频率分布直方图,如图所示.
某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据进行分组,分组区间为:[50,60),[60,70),[70,80),[80,90),[90,100],并绘制出频率分布直方图,如图所示.