题目内容
求曲线xy=1及直线y=x,y=3所围成图形的面积.
考点:定积分在求面积中的应用
专题:计算题,导数的概念及应用
分析:确定曲线交点的坐标,确定被积区间及被积函数,利用定积分表示面积,即可得到结论.
解答:
 解:由xy=1,y=3可得交点坐标为(
解:由xy=1,y=3可得交点坐标为(
,3),
由xy=1,y=x可得交点坐标为(1,1),
由y=x,y=3可得交点坐标为(3,3),
∴由曲线xy=1,直线y=x,y=3所围成的平面图形的面积为
(3-
)dx+
(3-x)dx=(3x-lnx)
+(3x-
x2)
=(3-1-ln3)+(9-
-3+
)=4-ln3.
 解:由xy=1,y=3可得交点坐标为(
解:由xy=1,y=3可得交点坐标为(| 1 |
| 3 |
由xy=1,y=x可得交点坐标为(1,1),
由y=x,y=3可得交点坐标为(3,3),
∴由曲线xy=1,直线y=x,y=3所围成的平面图形的面积为
| ∫ | 1
|
| 1 |
| x |
| ∫ | 3 1 |
| | | 1
|
| 1 |
| 2 |
| | | 3 1 |
| 9 |
| 2 |
| 1 |
| 2 |
点评:本题考查面积的计算,解题的关键是确定曲线交点的坐标,确定被积区间及被积函数,利用定积分表示面积.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
设i为虚数单位,则
等于( )
| -2i |
| 1-i |
| A、1-i | B、1+i |
| C、-1+i | D、-1-i |
复数z=
(i为虚数单位)的共轭复数为( )
| 1+2i |
| i |
| A、2-i | B、2+i |
| C、-2+i | D、-2-i |
已知集合A={x|
≥0},集合B={y|y=sinx,x∈R},则B∩CRA=( )
| 1+x |
| 1-x |
| A、∅ | B、{1} |
| C、{-1} | D、{-1,1} |
在星期一至星期五的5天内安排语、数、英三科测试,每天最多进行一门考试,且语文和数学不能连续两天考试,那么不同的考试安排方案种数共有( )
| A、18 | B、36 | C、12 | D、48 |
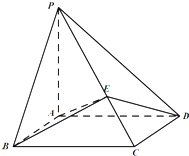 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=