题目内容
设二次函数f(x)=x2+x,当x∈[n,n+1](n∈N*)时,f(x)的所有整数值的个数为 (用n表示).
考点:二次函数的性质
专题:函数的性质及应用
分析:根据二次函数f(x)=x2+x的图象形状,分析出当x∈[n,n+1](n∈N*)时,f(x)的单调性和最值,进而可得答案.
解答:
解:二次函数f(x)=x2+x的图象是开口向上,且以直线x=-
为对称轴的抛物线
故当x∈[n,n+1](n∈N*)时,f(x)为增函数
当x=n时,函数f(x)取最小值n2+n;
当x=n+1时,函数f(x)取最大值(n+1)2+n+1=n2+3n+2;
故f(x)的所有整数值的个数为(n2+3n+2)-(n2+n)+1=2n+3个
故答案为:2n+3(n∈N*)
| 1 |
| 2 |
故当x∈[n,n+1](n∈N*)时,f(x)为增函数
当x=n时,函数f(x)取最小值n2+n;
当x=n+1时,函数f(x)取最大值(n+1)2+n+1=n2+3n+2;
故f(x)的所有整数值的个数为(n2+3n+2)-(n2+n)+1=2n+3个
故答案为:2n+3(n∈N*)
点评:本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,特别是开口方向和对称轴,是解答的关键.

练习册系列答案
相关题目
设向量
,
不共线,
=3(
+
),
=
-
,
=2
+
,给出下列结论:
①A,B,C共线;
②A,B,D共线;
③B,C,D共线;
④A,C,D共线,
其中所有正确结论的序号为 .
| e1 |
| e2 |
| AB |
| e1 |
| e2 |
| CB |
| e2 |
| e1 |
| CD |
| e1 |
| e2 |
①A,B,C共线;
②A,B,D共线;
③B,C,D共线;
④A,C,D共线,
其中所有正确结论的序号为
下列判断错误的是( )
| A、命题“?x∈R,2x>0”的否定是“?x0∈R,2x0≤0” | ||||
| B、命题“若xy=0,则x=0”的否命题为“若xy≠0,则x≠0” | ||||
C、“sinα=
| ||||
| D、函数y=2x-3+1的图象恒过定点A(3,2) |
设集合S={0,a},T={x∈Z|x2<2},则“a=1”是“S⊆T”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
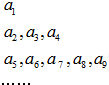 将数列{an}中的所有项按每一行比上一行多两项的规则排列成如图数表,已知图中的第一列数a1,a2,a5…构成一个等差数列,记为数列{bn},且b2=4,b5=10,图中每一行正中间一个数a1,a3,a7…构成数列{cn},其前n项和为Sn.
将数列{an}中的所有项按每一行比上一行多两项的规则排列成如图数表,已知图中的第一列数a1,a2,a5…构成一个等差数列,记为数列{bn},且b2=4,b5=10,图中每一行正中间一个数a1,a3,a7…构成数列{cn},其前n项和为Sn.