题目内容
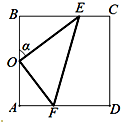 某休闲农庄有一块长方形鱼塘ABCD,AB=50米,BC=25
某休闲农庄有一块长方形鱼塘ABCD,AB=50米,BC=25| 3 |
(1)设∠BOE=α,试将△OEF的周长l表示成α的函数关系式,并求出此函数的定义域;
(2)经核算,三条走廊每米建设费用均为4000元,试问如何设计才能使建设总费用最低并求出最低总费用.
考点:函数模型的选择与应用,函数解析式的求解及常用方法
专题:应用题,函数的性质及应用
分析:(1)要将△OEF的周长l表示成α的函数关系式,需把△OEF的三边分别用含有α的关系式来表示,而OE,
OF,分别可以在Rt△OBE,Rt△OAF中求解,利用勾股定理可求EF,从而可求.
(2)要求铺路总费用最低,只要求△OEF的周长l的最小值即可.由(1)得l=
,α∈[
,
],
利用换元,设sinα+cosα=t,则sinαcosα=
,从而转化为求函数在闭区间上的最小值.
OF,分别可以在Rt△OBE,Rt△OAF中求解,利用勾股定理可求EF,从而可求.
(2)要求铺路总费用最低,只要求△OEF的周长l的最小值即可.由(1)得l=
| 25(sinα+cosα+1) |
| cosαsinα |
| π |
| 6 |
| π |
| 3 |
利用换元,设sinα+cosα=t,则sinαcosα=
| t2-1 |
| 2 |
解答:
解:(1)∵在Rt△BOE中,OB=25,∠B=90°,∠BOE=α,
∴OE=
在Rt△AOF中,OA=25,∠A=90°,∠AFO=α,
∴OF=
.
又∠EOF=90°,
∴EF=
=
,
∴l=OE+OF+EF=
.
当点F在点D时,这时角α最小,此时α=
;
当点E在C点时,这时角α最大,求得此时α=
.
故此函数的定义域为[
,
];
(2)由题意知,要求铺路总费用最低,只要求△OEF的周长l的最小值即可.
由(1)得,l=
,α∈[
,
],
设sinα+cosα=t,则sinαcosα=
,
∴l=
=
由t=sinα+cosα=
sin(α+
),
又
≤α+
≤
,得
≥t≤
,
∴
≤t-1≤
-1,
从而当α=
,即BE=25时,lmin=50(
+1),
所以当BE=AF=25米时,铺路总费用最低,最低总费用为200000(
+1)元.
∴OE=
| 25 |
| cosα |
在Rt△AOF中,OA=25,∠A=90°,∠AFO=α,
∴OF=
| 25 |
| sinα |
又∠EOF=90°,
∴EF=
| OE2+OF2 |
| 25 |
| cosαsinα |
∴l=OE+OF+EF=
| 25(sinα+cosα+1) |
| cosαsinα |
当点F在点D时,这时角α最小,此时α=
| π |
| 6 |
当点E在C点时,这时角α最大,求得此时α=
| π |
| 3 |
故此函数的定义域为[
| π |
| 6 |
| π |
| 3 |
(2)由题意知,要求铺路总费用最低,只要求△OEF的周长l的最小值即可.
由(1)得,l=
| 25(sinα+cosα+1) |
| cosαsinα |
| π |
| 6 |
| π |
| 3 |
设sinα+cosα=t,则sinαcosα=
| t2-1 |
| 2 |
∴l=
| 25(sinα+cosα+1) |
| cosαsinα |
| 50 |
| t-1 |
由t=sinα+cosα=
| 2 |
| π |
| 4 |
又
| 5π |
| 12 |
| π |
| 4 |
| 7π |
| 12 |
| ||
| 2 |
| 2 |
∴
| ||
| 2 |
| 2 |
从而当α=
| π |
| 4 |
| 2 |
所以当BE=AF=25米时,铺路总费用最低,最低总费用为200000(
| 2 |
点评:本题主要考查了借助于三角函数解三角形在实际问题中的应用,考查了利用数学知识解决实际问题的能力,及推理运算的能力.

练习册系列答案
相关题目
已知集合A={x|y=
}},B={y|y=-x2+2x-1},则A∩B=( )
| lg(2-x) | ||
|
| A、(-3,0] |
| B、[-3,-2] |
| C、(-∞,-3) |
| D、(-3,-2] |
已知正数x,y满足x+y+
+
=5,则x+y的取值范围是( )
| 1 |
| x |
| 1 |
| y |
| A、[2,3] | ||
B、[
| ||
| C、[1,4] | ||
| D、[1,5] |
直线3x+4y-9=0与圆x2+(y-1)2=1的位置关系是( )
| A、相离 |
| B、相切 |
| C、直线与圆相交且过圆心 |
| D、直线与圆相交但不过圆心 |
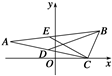 如图,已知△ABC中A(-8,2),AB边上中线CE所在直线的方程为x+2y-5=0,AC边上的中线BD所在直线的方程为2x-5y+8=0,求直线BC的方程.
如图,已知△ABC中A(-8,2),AB边上中线CE所在直线的方程为x+2y-5=0,AC边上的中线BD所在直线的方程为2x-5y+8=0,求直线BC的方程.