题目内容
设数列{an}的前n项和为Sn=n2,则a9的值是 .
考点:数列递推式
专题:等差数列与等比数列
分析:由已知得a9=S9-S8,由此能求出结果.
解答:
解:∵数列{an}的前n项和为Sn=n2,
∴a9=S9-S8=92-82=17.
故答案为:17.
∴a9=S9-S8=92-82=17.
故答案为:17.
点评:本题考查数列的第9项的求法,是基础题,解题时要注意公式an=
的合理运用.
|

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
正整数指数函数y=(a+1)x是x∈N上的减函数,则a的取值范围是( )
| A、0<a<1 | B、-1<a<0 |
| C、a>0 | D、a≥0 |
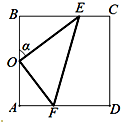 某休闲农庄有一块长方形鱼塘ABCD,AB=50米,BC=25
某休闲农庄有一块长方形鱼塘ABCD,AB=50米,BC=25