题目内容
若loga2=m，loga3=n，其中a＞0，且a≠1，则am-n= ．
考点：对数的运算性质
专题：函数的性质及应用
分析：化对数式为指数式，然后利用有理指数幂的运算性质化简求值．
解答：
解：∵loga2=m，loga3=n，
∴am=2，an=3，
则am-n=
=
．
故答案为：
．
∴am=2，an=3，
则am-n=
| am |
| an |
| 2 |
| 3 |
故答案为：
| 2 |
| 3 |
点评：本题考查了对数的运算性质，考查了有理指数幂的化简求值，是基础题．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
直线y=x与曲线xy=1的交点坐标是（ ）
| A、（1，1） |
| B、（1，1）和（-1，-1） |
| C、（-1，-1） |
| D、（0，0） |
在自然界中，存在着大量的周期函数，比如声波，若两个声波随时间的变化规律分别为：y1=3sin（100πt），y2=3cos（100πt），则这两个声波合成后即y=y1+y2的振幅为（ ）
| A、3 | ||
| B、6 | ||
C、3
| ||
D、6
|
设全集U={0，1，2，3}，集合M={0，1，2}，N={0，2，3}，则M∩∁UN等于（ ）
| A、{1} | B、{2，3} |
| C、{0，1，2} | D、φ |
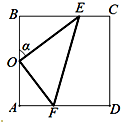某休闲农庄有一块长方形鱼塘ABCD，AB=50米，BC=25