题目内容
已知正数x,y满足x+y+
+
=5,则x+y的取值范围是( )
| 1 |
| x |
| 1 |
| y |
| A、[2,3] | ||
B、[
| ||
| C、[1,4] | ||
| D、[1,5] |
考点:基本不等式在最值问题中的应用
专题:综合题,不等式的解法及应用
分析:由x+y+
+
=5,可得(x+y)(x+y+
+
)=5(x+y),结合基本不等式,即可求出x+y的取值范围.
| 1 |
| x |
| 1 |
| y |
| 1 |
| x |
| 1 |
| y |
解答:
解:∵x+y+
+
=5,
∴(x+y)(x+y+
+
)=5(x+y),
∴(x+y)2+
+
+2=5(x+y),
∴5(x+y)≥(x+y)2+4,
即(x+y)2-5(x+y)+4≤0
解得1≤x+y≤4,
故选:C.
| 1 |
| x |
| 1 |
| y |
∴(x+y)(x+y+
| 1 |
| x |
| 1 |
| y |
∴(x+y)2+
| y |
| x |
| x |
| y |
∴5(x+y)≥(x+y)2+4,
即(x+y)2-5(x+y)+4≤0
解得1≤x+y≤4,
故选:C.
点评:本题考查基本不等式的运用,考查学生的计算能力,正确运用基本不等式是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设全集U={0,1,2,3},集合M={0,1,2},N={0,2,3},则M∩∁UN等于( )
| A、{1} | B、{2,3} |
| C、{0,1,2} | D、φ |
正整数指数函数y=(a+1)x是x∈N上的减函数,则a的取值范围是( )
| A、0<a<1 | B、-1<a<0 |
| C、a>0 | D、a≥0 |
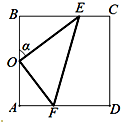 某休闲农庄有一块长方形鱼塘ABCD,AB=50米,BC=25
某休闲农庄有一块长方形鱼塘ABCD,AB=50米,BC=25