题目内容
6.求下列函数的定义域:(1)y=tanx+$\frac{1}{tanx}$;
(2)y=$\sqrt{sinx}$+tanx.
分析 根据函数成立的条件结合三角函数的取值范围进行求解即可.
解答 解:(1)要使函数有意义,则$\left\{\begin{array}{l}{tanx≠0}\\{x≠kπ+\frac{π}{2},k∈Z}\end{array}\right.$,
即$\left\{\begin{array}{l}{x≠kπ}\\{x≠kπ+\frac{π}{2},k∈Z}\end{array}\right.$,
即x≠kπ且x≠kπ+$\frac{π}{2}$,即函数的定义域为{x|x≠kπ且x≠kπ+$\frac{π}{2}$},k∈Z.
(2)要使函数有意义,则$\left\{\begin{array}{l}{sinx≥0}\\{x≠kπ+\frac{π}{2}}\end{array}\right.$,
即$\left\{\begin{array}{l}{2kπ≤x≤2kπ+π}\\{x≠kπ+\frac{π}{2}}\end{array}\right.$,k∈Z,
则2kπ≤x≤2kπ+π,且x≠2kπ+$\frac{π}{2}$,k∈Z
即函数的定义域为{x|2kπ≤x≤2kπ+π,且x≠2kπ+$\frac{π}{2}$},k∈Z.
点评 本题主要考查函数的定义域的求解,根据三角函数的取值范围建立不等式关系是解决本题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
14.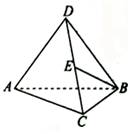 如图,在三棱锥D-ABC中,∠ABC=90°,平面DAB⊥平面ABC,DA=AB=DB=BC,E是DC的中点,则AC与BE所成角的余弦值为( )
如图,在三棱锥D-ABC中,∠ABC=90°,平面DAB⊥平面ABC,DA=AB=DB=BC,E是DC的中点,则AC与BE所成角的余弦值为( )
 如图,在三棱锥D-ABC中,∠ABC=90°,平面DAB⊥平面ABC,DA=AB=DB=BC,E是DC的中点,则AC与BE所成角的余弦值为( )
如图,在三棱锥D-ABC中,∠ABC=90°,平面DAB⊥平面ABC,DA=AB=DB=BC,E是DC的中点,则AC与BE所成角的余弦值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{{\sqrt{15}}}{16}$ | D. | $\frac{1}{3}$ |
1.已知函数f(x)=ax-ln x,若f(x)>1在区间(1,+∞)内恒成立,则实数a的取值范围是( )
| A. | (-∞,1) | B. | (-∞,1] | C. | (1,+∞) | D. | [1,+∞) |
18.一个几何体的三视图及其尺寸如图(单位:cm),则该几何体的体积是( )cm3


| A. | 20π | B. | 16π | C. | 15π | D. | 12π |