题目内容
11.若A={x|mx2+x+m=0,m∈R},且A∩R=∅,则实数m的取值范围为(-∞,-$\frac{1}{2}$)∪($\frac{1}{2}$,+∞).分析 由已知得mx2+x+m=0无解,从而$\left\{\begin{array}{l}{m≠0}\\{△=1-4{m}^{2}<0}\end{array}\right.$,由此能求出实数m的取值范围.
解答 解:∵A={x|mx2+x+m=0,m∈R},且A∩R=∅,
∴mx2+x+m=0无解,
∴$\left\{\begin{array}{l}{m≠0}\\{△=1-4{m}^{2}<0}\end{array}\right.$,
解得m<-$\frac{1}{2}$或m>$\frac{1}{2}$.
∴实数m的取值范围是(-∞,-$\frac{1}{2}$)∪($\frac{1}{2}$,+∞).
故答案为:(-∞,-$\frac{1}{2}$)∪($\frac{1}{2}$,+∞).
点评 本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意交集定义的合理运用.

练习册系列答案
相关题目
1.已知复数$z=\frac{5-i}{1-i}$,则z的虚部为( )
| A. | 2i | B. | 3i | C. | 2 | D. | 3 |
19.若f(x)=log3x,则f′(3)等于( )
| A. | $\frac{1}{3}$ | B. | ln 3 | C. | $\frac{1}{3ln3}$ | D. | $\frac{1}{ln3}$ |
3.如图可能是下列哪个函数的图象( )
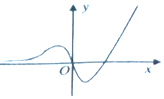

| A. | y=2x-x2-1 | B. | $y=\frac{{{2^x}sinx}}{4x+1}$ | C. | $y=\frac{x}{lnx}$ | D. | y=(x2-2x)ex |