题目内容
曲线5x2-ky2=5的焦距为4,那么k的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:椭圆的标准方程,双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:先把曲线5x2-ky2=5化为标准形式,分曲线5x2-ky2=5是椭圆和曲线5x2-ky2=5是双曲线两种情况进行分类讨论,能求出k的值.
解答:
解:曲线5x2-ky2=5化为标准形式,得x2-
=1,
∵曲线5x2-ky2=5的焦距为4,
∴当曲线5x2-ky2=5是椭圆时,
=2,解得k=-1;
当曲线5x2-ky2=5是双曲线时,
=2,解得k=
.
∴k的值为
或-1.
故选:C.
| y2 | ||
|
∵曲线5x2-ky2=5的焦距为4,
∴当曲线5x2-ky2=5是椭圆时,
-
|
当曲线5x2-ky2=5是双曲线时,
1+
|
| 5 |
| 3 |
∴k的值为
| 5 |
| 3 |
故选:C.
点评:本题考查实数k的值的求法,是中档题,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
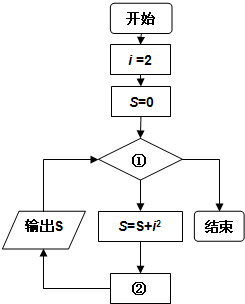 如图是表示输出22,22+42,22+42+62,…,22+42+62+…+20042的值的过程的一个程序框图,那么在图中①、②处应分别填上( )
如图是表示输出22,22+42,22+42+62,…,22+42+62+…+20042的值的过程的一个程序框图,那么在图中①、②处应分别填上( )| A、i≤2014,i=i+2 |
| B、i≤1007,i=i+2 |
| C、i≤2014,i=i+1 |
| D、i≤1007,i=i+1 |
已知实数x,y满足x+4y=1,则xy的值域为( )
A、(0,
| ||||
B、[-
| ||||
C、(-∞,
| ||||
D、(-∞,
|
若直线l上不同的三个点A,B,C与直线l外一点O,使得x2
+x
=2
成立,则满足条件的实数x的集合为( )
| OA |
| OB |
| BC |
| A、{-1,0} | ||||||||
B、{
| ||||||||
C、{
| ||||||||
| D、{-1} |
若
,
不同为零向量,则条件“存在实数λ,使得
=λ
”是“
∥
”的( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设集合M={x|2x<
},N={x|-2≤x≤3},则M∩N=( )
| 1 |
| 2 |
| A、[-2,1) |
| B、[-2,-l) |
| C、(-1,3] |
| D、[-2,3] |
已知一几何体三视图如图,则其体积为( )
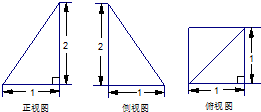

A、
| ||
B、
| ||
| C、1 | ||
| D、2 |