题目内容
15.下列函数中,既是偶函数,又在区间(0,3)内是减函数的是( )| A. | y=2x-2-x | B. | y=cosx | C. | y=log2|x| | D. | y=x+x-1 |
分析 根据题意,依次分析选项,是否满足题目对单调性、奇偶性的要求,即可得答案.
解答 解:根据题意,依次分析选项:
对于A、y=2x-2-x,其定义域为R,有f(-x)=2-x-2x=-f(x),为奇函数,不符合题意;
对于B、y=cosx,定义域R,且有f(-x)=cos(-x)=cosx=f(x)为偶函数,且其在(0,π)上为减函数,符合题意;
对于C、y=log2|x|,有y=log2|x|=$\left\{\begin{array}{l}{lo{g}_{2}x,x>0}\\{lo{g}_{2}(-x),x<0}\end{array}\right.$,在(0,+∞)上为增函数,不符合题意;
对于D、y=x+x-1=x+$\frac{1}{x}$,在(0,1)为减函数,(1,+∞)为增函数,不符合题意;
故选:B.
点评 本题考查函数的奇偶性、单调性的判断,要掌握常见函数的奇偶性、单调性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.一个正四面体的棱长为2,则这个正四面体的外接球的表面积为( )
| A. | 6π | B. | 8π | C. | $\sqrt{6}π$ | D. | 11π |
6.函数f(x)在定义域R内可导,若f(x)=f(2-x),且当x∈(-∞,1)时,(x-1)f'(x)<0,设$a=f(-1),b=f(\frac{3}{2}),c=f(2)$则( )
| A. | a<b<c | B. | b<c<a | C. | a<c<b | D. | c<a<b |
4.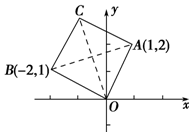 如图在复平面上,一个正方形的三个顶点对应的复数分别是1+2i,-2+i,0,那么这个正方形的第四个顶点对应的复数为( )
如图在复平面上,一个正方形的三个顶点对应的复数分别是1+2i,-2+i,0,那么这个正方形的第四个顶点对应的复数为( )
 如图在复平面上,一个正方形的三个顶点对应的复数分别是1+2i,-2+i,0,那么这个正方形的第四个顶点对应的复数为( )
如图在复平面上,一个正方形的三个顶点对应的复数分别是1+2i,-2+i,0,那么这个正方形的第四个顶点对应的复数为( )| A. | 3+i | B. | -1+3i | C. | 1-3i | D. | 3-i |
5.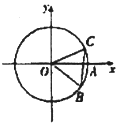 ∠AOB如图,⊙O与x轴的正半轴交点为A,点B,C在⊙O上,且$B(\frac{3}{5},-\frac{4}{5})$,点C在第一象限,∠AOC=α,BC=1,则$cos(\frac{5π}{6}-α)$=( )
∠AOB如图,⊙O与x轴的正半轴交点为A,点B,C在⊙O上,且$B(\frac{3}{5},-\frac{4}{5})$,点C在第一象限,∠AOC=α,BC=1,则$cos(\frac{5π}{6}-α)$=( )
 ∠AOB如图,⊙O与x轴的正半轴交点为A,点B,C在⊙O上,且$B(\frac{3}{5},-\frac{4}{5})$,点C在第一象限,∠AOC=α,BC=1,则$cos(\frac{5π}{6}-α)$=( )
∠AOB如图,⊙O与x轴的正半轴交点为A,点B,C在⊙O上,且$B(\frac{3}{5},-\frac{4}{5})$,点C在第一象限,∠AOC=α,BC=1,则$cos(\frac{5π}{6}-α)$=( )| A. | $-\frac{4}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |