题目内容
19．关于复数Z=$\frac{2}{-1+i}$的四个命题：p1：|Z|=2
p2：Z2=2i
p3：Z的共轭复数为1+i
p4：Z的虚部为-1．
其中的真命题为（ ）
| A． | p2，p3 | B． | p1，p2 | C． | p2，p4 | D． | p3，p4 |
分析 复数Z=$\frac{2}{-1+i}$=-1-i，再利用复数的有关概念及其运算即可判断出结论．
解答 解：复数Z=$\frac{2}{-1+i}$=$\frac{-2（1+i）}{（1-i）（1+i）}$=-1-i．
p1：|Z|=$\sqrt{（-1）^{2}+（-1）^{2}}$=$\sqrt{2}$≠2，因此不正确；
p2：Z2=2i，正确；
p3：Z的共轭复数为-1+i，因此不正确；
p4：Z的虚部为-1．正确．
其中的真命题个数为2．
故选：C．
点评 本题考查了复数的运算法则、模的计算公式等基础知识，考查了推理能力与计算能力，属于基础题．
练习册系列答案
暑假作业海燕出版社系列答案
相关题目
5．
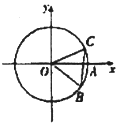∠AOB如图，⊙O与x轴的正半轴交点为A，点B，C在⊙O上，且$B（\frac{3}{5}，-\frac{4}{5}）$，点C在第一象限，∠AOC=α，BC=1，则$cos（\frac{5π}{6}-α）$=（ ）
∠AOB如图，⊙O与x轴的正半轴交点为A，点B，C在⊙O上，且$B（\frac{3}{5}，-\frac{4}{5}）$，点C在第一象限，∠AOC=α，BC=1，则$cos（\frac{5π}{6}-α）$=（ ）| A． | $-\frac{4}{5}$ | B． | $-\frac{3}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
10．已知A、B、C、D四点共线，$α∈（\frac{π}{2}，π）$，且向量$\overrightarrow{AB}=（tanα，1）$，$\overrightarrow{CD}=（3tan2α，-2）$，则$tan（2α-\frac{π}{4}）$等于（ ）
| A． | $-\frac{1}{7}$ | B． | $\frac{1}{7}$ | C． | -7 | D． | 7 |
7．已知函数$f（x）=lnx+\frac{1}{2}{x^2}-ax+1$，下列结论中错误的是（ ）
| A． | 当a=2时，x=1是f（x）的一个极值点 | B． | 当-2＜a＜2时，函数f（x）无极值 | ||
| C． | 当a＞2时，f（x）的极小值小于0 | D． | ?a∈R，f（x）必有零点 |
11．已知命题p：“?x∈（0，+∞），lnx+4x≥3”；命题q：“?x0∈（0，+∞），8x0+$\frac{1}{2{x}_{0}}$≤4”．则下列命题为真命题的是（ ）
| A． | （￢p）∧q | B． | p∧q | C． | p∨（￢q） | D． | （￢p）∧（￢q） |
8．圆O1：x2+y2-2x=0和圆O2：x2+y2-4x=0的公切线条数（ ）
| A． | 1条 | B． | 2条 | C． | 3条 | D． | 4条 |