题目内容
由直线y=0，x=e，y=2x及曲线y=
所围成的封闭的图形的面积为（ ）
| 2 |
| x |
| A、3 |
| B、3+2ln2 |
| C、e2-3 |
| D、e |
考点：定积分在求面积中的应用
专题：计算题,导数的概念及应用
分析：先联立两个曲线的方程，求出交点，以确定积分公式中x的取值范围，最后根据定积分的几何意义表示出区域的面积，根据定积分公式解之即可．
解答：
解：由y=2x及曲线y=
，可得交点坐标为（1，2），（-1，-2），
故所求图形的面积为S=
(2x-
)dx=（x2-2lnx）
=e2-3．
故选：C．
| 2 |
| x |
故所求图形的面积为S=
| ∫ | e 1 |
| 2 |
| x |
| | | e 1 |
故选：C．
点评：本题主要考查了定积分在求面积中的应用，以及定积分的计算，属于基础题．
练习册系列答案
名师点拨卷系列答案
相关题目
现将甲乙丙丁4个不同的小球放入A、B、C三个盒子中，要求每个盒子至少放1个小球，且小球甲不能放在A盒中，则不同的放法有（ ）
| A、12种 | B、24种 |
| C、36种 | D、72种 |
已知l是直线，α、β是两个不同平面，下列命题中的真命题是（ ）
| A、若l∥α，l∥β，则α∥β |
| B、若α⊥β，l∥α，则l⊥β |
| C、若l⊥α，l∥β，则α⊥β |
| D、若l∥α，α∥β，则l∥β |
正方形ABCD的边长为3，点E在边AB上，点F在边BC上，AE=BF=1，动点P从点E出发沿直线向F运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角．当点P第一次碰到点E时，P与正方形的边碰撞的次数为（ ）
| A、8 | B、6 | C、4 | D、3 |
一个几何体的三视图及尺寸如图所示，则该几何体的体积为（ ）
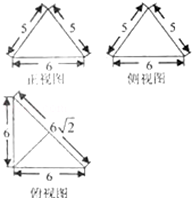
| A、48 | B、72 | C、12 | D、24 |
用反证法证明：“若a，b，c都是正数，则三个数a+
，b+
，c+
中至少有一个不小于2”时，“假设”应为（ ）
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
A、假设a+
| ||||||
B、假设a+
| ||||||
C、假设a+
| ||||||
D、假设a+
|
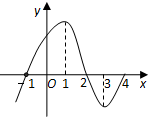如图所示为y=f′（x）的图象，则下列判断正确的是（ ）①f（x）在（-∞，1）上是增函数；
②x=-1是f（x）的极小值点；
③f（x）在（2，4）上是减函数，在（-1，2）上是增函数；
④x=2是f（x）的极小值点．
| A、①②③ | B、①③④ |
| C、③④ | D、②③ |
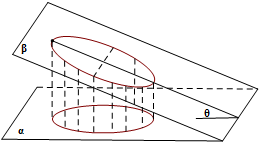如图，一个底面半径为R的圆柱被与其底面所成角为θ（00＜θ＜900）的平面所截，截面是一个椭圆．当θ为30°时，这个椭圆的离心率为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
