题目内容
9.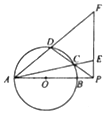 如图,AB是圆O的直径,P是线段AB延长线上一点,割线PCD交圆O于点C,D,过点P作AP的垂线,交线段AC的延长线于点E,交线段AD的延长线于点F,且PE•PF=5,PB=$\frac{1}{2}$OA.
如图,AB是圆O的直径,P是线段AB延长线上一点,割线PCD交圆O于点C,D,过点P作AP的垂线,交线段AC的延长线于点E,交线段AD的延长线于点F,且PE•PF=5,PB=$\frac{1}{2}$OA.(1)求证:C,D,E,F四点共圆;
(2)求圆O的面积.
分析 (1)连结BD,AB是圆O的直径,可得∠BDA=90°,由同弧所对圆周角相等可得∠CDB=∠CAB,证得∠PEC=∠PDF,即可得到四点共圆;
(2)设出圆O的半径为r,利用割线定理,解方程可得r=2,再由圆的面积公式计算即可得到所求值.
解答 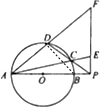 (1)证明:连结BD,AB是圆O的直径,
(1)证明:连结BD,AB是圆O的直径,
直径所对圆周角为直角可得∠BDA=90°,
由同弧所对圆周角相等,可得∠CDB=∠CAB,
又∠PEC=90°-∠CAB,
∠PDF=90°-∠CDB,
可得:∠PEC=∠PDF,
故D,C,E,F四点共圆;
(2)解:设圆O的半径为r,
由圆的割线定理可得,
PE•PF=PC•PD=PB•PA=$\frac{1}{2}$r(2r+$\frac{1}{2}$r)=5,
解得r=2,
可得圆O的面积为4π.
点评 本题考查四点共圆的证明,注意运用圆的同弧所对圆周角相等,以及直径所对圆周角为直角,考查割线定理的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
19.已知集合A={x|1<x≤3},B={x|x<4,x∈Z},则A∩B=( )
| A. | (2,3) | B. | [2,3] | C. | {2,3} | D. | {2,3,4} |
17.集合P={x||x|>1},Q={x|y=$\sqrt{4-{x}^{2}}$},则P∩Q=( )
| A. | [-2,-1] | B. | (1,2) | C. | [-2,-1)∪(1,2] | D. | [-2,2] |
14.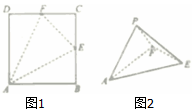 如图1,ABCD是边长为2的正方形,点E,F分别为BC,CD的中点,将△ABE,△ECF,△FDA分别沿AE,EF,FA折起,使B,C,D三点重合于点P,若四面体PAEF的四个顶点在同一个球面上,则该球的表面积是( )
如图1,ABCD是边长为2的正方形,点E,F分别为BC,CD的中点,将△ABE,△ECF,△FDA分别沿AE,EF,FA折起,使B,C,D三点重合于点P,若四面体PAEF的四个顶点在同一个球面上,则该球的表面积是( )
 如图1,ABCD是边长为2的正方形,点E,F分别为BC,CD的中点,将△ABE,△ECF,△FDA分别沿AE,EF,FA折起,使B,C,D三点重合于点P,若四面体PAEF的四个顶点在同一个球面上,则该球的表面积是( )
如图1,ABCD是边长为2的正方形,点E,F分别为BC,CD的中点,将△ABE,△ECF,△FDA分别沿AE,EF,FA折起,使B,C,D三点重合于点P,若四面体PAEF的四个顶点在同一个球面上,则该球的表面积是( )| A. | $\sqrt{6}π$ | B. | 6π | C. | $4\sqrt{3}π$ | D. | 12π |
19.双曲线上存在一点与其中心及一个焦点构成等边三角形,则此双曲线的离心率为( )
| A. | 2 | B. | $\sqrt{3}$+1 | C. | $\sqrt{3}$ | D. | $\sqrt{3}$-1 |
 如图,在△ABC中,CA=2,CB=1,CD是AB边上的中线.
如图,在△ABC中,CA=2,CB=1,CD是AB边上的中线.