题目内容
19.双曲线上存在一点与其中心及一个焦点构成等边三角形,则此双曲线的离心率为( )| A. | 2 | B. | $\sqrt{3}$+1 | C. | $\sqrt{3}$ | D. | $\sqrt{3}$-1 |
分析 根据正三角形的性质得到三角形F1PF2为直角三角形,利用双曲线离心率的定义进行求解即可.
解答  解:如图P,与坐标原点O,右焦点F2构成正三角形,
解:如图P,与坐标原点O,右焦点F2构成正三角形,
连接PF1,则三角形F1PF2为直角三角形,
则PF2=c,PF1=PF2tan60°=$\sqrt{3}$c,
由双曲线的定义可得PF1-PF2=2a,
∴($\sqrt{3}$-1)c=2a,
则e=$\frac{c}{a}$=$\frac{2}{\sqrt{3}-1}$=$\sqrt{3}$+1,
故选:B.
点评 本题主要考查双曲线离心率的计算,根据直角三角形的性质建立方程关系是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.已知向量$\overrightarrow a,\overrightarrow b$满足|$\overrightarrow a}|=2,|{\overrightarrow b}$|=2,|$\overrightarrow{b}$|=1,且($\overrightarrow a+3\overrightarrow b})⊥({2\overrightarrow a-\overrightarrow b}$)⊥(2$\overrightarrow{a}$-$\overrightarrow{b}$),则$\overrightarrow a,\overrightarrow b$的夹角为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
11.已知点F(2,0)是双曲线3x2-my2=3m(m>0)的一个焦点,则此双曲线的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
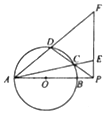 如图,AB是圆O的直径,P是线段AB延长线上一点,割线PCD交圆O于点C,D,过点P作AP的垂线,交线段AC的延长线于点E,交线段AD的延长线于点F,且PE•PF=5,PB=$\frac{1}{2}$OA.
如图,AB是圆O的直径,P是线段AB延长线上一点,割线PCD交圆O于点C,D,过点P作AP的垂线,交线段AC的延长线于点E,交线段AD的延长线于点F,且PE•PF=5,PB=$\frac{1}{2}$OA.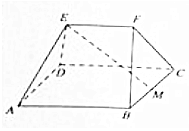 如图,在多面体ABCDEF中,四边形ABCD为边长为4的正方形,M是BC的中点,EF∥平面ABCD,且EF=2,AE=DE=BF=CF=$2\sqrt{2}$.
如图,在多面体ABCDEF中,四边形ABCD为边长为4的正方形,M是BC的中点,EF∥平面ABCD,且EF=2,AE=DE=BF=CF=$2\sqrt{2}$.