题目内容
4.(2$\sqrt{x}$-$\frac{1}{\root{4}{x}}$)6的展开式的常数项是60(用数字作答)分析 利用通项公式即可得出.
解答 解:通项公式Tr+1=${∁}_{6}^{r}(2\sqrt{x})^{6-r}(-\frac{1}{\root{4}{x}})^{r}$=(-1)r26-r${∁}_{6}^{r}$${x}^{3-\frac{3r}{4}}$,
令3-$\frac{3r}{4}$=0,解得r=4.
∴常数项是${2}^{2}{∁}_{6}^{4}$=60.
故答案为:60.
点评 本题考查了二项式定理的性质及其应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
19.在△ABC中,BC:AB=2:$\sqrt{3}$,∠B=30°,则∠C=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
16.已知α,β,γ是三个不同的平面,l,m是两条不同的直线,则下列命题一定正确的是( )
| A. | 若l丄α,l∥β则 α∥β | |
| B. | 若γ丄α,γ丄β,则 α∥β | |
| C. | 若l∥m且 l?α,m?β,l∥β,m∥α,则 α∥β | |
| D. | 若l,m 异面,且 l?α,m?β,l∥β,m∥α,则 α∥β |
13.为防止某种疾病,今研制一种新的预防药,任选取100只小白鼠作试验,得到如下的列联表:
K2的观测值为3.2079,则在犯错误的概率不超过( )的前提下认为“药物对防止某种疾病有效”.
参考数据:
| 患病 | 未患病 | 总计 | |
| 服用药 | 15 | 40 | 55 |
| 没服用药 | 20 | 25 | 45 |
| 总计 | 35 | 65 | 100 |
参考数据:
| P( K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 0.025 | B. | 0.05 | C. | 0.010 | D. | 0.10 |
14.已知向量$\overrightarrow a,\overrightarrow b$满足|$\overrightarrow a}|=2,|{\overrightarrow b}$|=2,|$\overrightarrow{b}$|=1,且($\overrightarrow a+3\overrightarrow b})⊥({2\overrightarrow a-\overrightarrow b}$)⊥(2$\overrightarrow{a}$-$\overrightarrow{b}$),则$\overrightarrow a,\overrightarrow b$的夹角为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
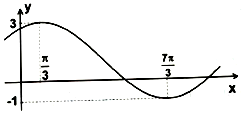 已知如图为f(x)=msin(ωx+φ)+n,m>0,ω>0的图象.
已知如图为f(x)=msin(ωx+φ)+n,m>0,ω>0的图象. 如图,六棱锥P-ABCDEF的底面是边长为1的正六边形,PA⊥底面ABCDEF.
如图,六棱锥P-ABCDEF的底面是边长为1的正六边形,PA⊥底面ABCDEF.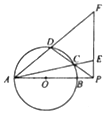 如图,AB是圆O的直径,P是线段AB延长线上一点,割线PCD交圆O于点C,D,过点P作AP的垂线,交线段AC的延长线于点E,交线段AD的延长线于点F,且PE•PF=5,PB=$\frac{1}{2}$OA.
如图,AB是圆O的直径,P是线段AB延长线上一点,割线PCD交圆O于点C,D,过点P作AP的垂线,交线段AC的延长线于点E,交线段AD的延长线于点F,且PE•PF=5,PB=$\frac{1}{2}$OA.