题目内容
18.已知圆C1:x2+y2=4和圆C2:(x-2)2+(y-2)2=4,若点P(a,b)(a>0,b>0)在两圆的公共弦上,则$\frac{1}{a}+\frac{9}{b}$的最小值为8.分析 求出两圆的公共弦,再利用基本不等式,即可得出结论.
解答 解:由题意,两圆的方程相减,可得x+y=2,
∵点P(a,b)(a>0,b>0)在两圆的公共弦上,
∴a+b=2,
∴$\frac{1}{a}+\frac{9}{b}$=$\frac{1}{2}$($\frac{1}{a}+\frac{9}{b}$)(a+b)=$\frac{1}{2}$(10+$\frac{b}{a}$+$\frac{9a}{b}$)$≥\frac{1}{2}(10+6)$=8,
当且仅当$\frac{b}{a}$=$\frac{9a}{b}$,即b=3a时,取等号,$\frac{1}{a}+\frac{9}{b}$的最小值为8,
故答案为8.
点评 本题考查圆与圆的位置关系,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
13.“α=$\frac{π}{6}$”是$tan({π-a})=-\frac{{\sqrt{3}}}{3}$的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
3.已知$f(x)=cos({ωx+\frac{π}{3}})$,且ω是函数y=ex-e2x的极值点,则f(x)的一条对称轴是( )
| A. | $x=-\frac{π}{3}$ | B. | $x=\frac{π}{3}$ | C. | $x=\frac{π}{6}$ | D. | $x=\frac{2π}{3}$ |
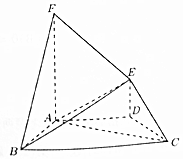 在如图所示的多面体中,DE⊥平面ABCD,AF∥DE,AD∥BC,AB=CD,∠ABC=60°,BC=2AD=4DE=4.
在如图所示的多面体中,DE⊥平面ABCD,AF∥DE,AD∥BC,AB=CD,∠ABC=60°,BC=2AD=4DE=4.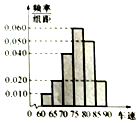 交警随机抽取了途经某服务站的40辆小型轿车在经过某区间路段的车速(单位:km/h),现将其分成六组为[60,65),[65,70),[70,75),[75,80),[80,85),[85,90]后得到如图所示的频率分布直方图.
交警随机抽取了途经某服务站的40辆小型轿车在经过某区间路段的车速(单位:km/h),现将其分成六组为[60,65),[65,70),[70,75),[75,80),[80,85),[85,90]后得到如图所示的频率分布直方图.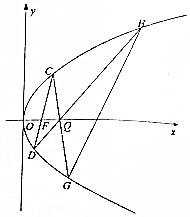 在直角坐标系xOy中,设抛物线E:y2=2px(p>0)的焦点为F,准线为直线l,点A、B在直线l上,点M为抛物线E第一象限上的点,△ABM是边长为$\frac{8}{3}$$\sqrt{3}$的等边三角形,直线MF的倾斜角为60°.
在直角坐标系xOy中,设抛物线E:y2=2px(p>0)的焦点为F,准线为直线l,点A、B在直线l上,点M为抛物线E第一象限上的点,△ABM是边长为$\frac{8}{3}$$\sqrt{3}$的等边三角形,直线MF的倾斜角为60°.