题目内容
已知函数f(x)=x3-3x2+bx+c在x=1处的切线是y=(3a-3)x-3a+4.
(1)试用a表示b和c;
(2)求函数f(x)≥-
在[1,3]上恒成立,求实数a的取值范围.
(1)试用a表示b和c;
(2)求函数f(x)≥-
| 3 |
| 2 |
考点:利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)先求出函数f(x)的导数f′(x),求出f′(1),根据条件求出f(1),列出方程,得到b=3a,c=3-3a;
(2)求参数a的取值范围,实际上就是求参数的最值问题.
(2)求参数a的取值范围,实际上就是求参数的最值问题.
解答:
解:(1)∵为f'(x)=3x2-6x+b,
∴f'(1)=-3+b=3a-3,f(1)=b+c-2=1,
即有b=3a,c=-3a+3.
(2)由(1)可知f(x)=x3-3x2+3ax-3a+3,
x3-3x2+3ax-3a+3≥-
,
3ax-3a≥-x3+3x2-
,
3a(x-1)≥-x3+3x2-
,
当x=1时,成立,a∈R,
当x≠1时,3a≥
,
令t=x-1,3a≥
=-t2+3-
令g(t)=-t2+3-
,(0<t≤2),
∴以g′(t)=-2t+
=
,g′(t)>0⇒t<(
)
,g′(t)<0⇒t>(
)
,
g(t)max=g((
)
)=3-3(
)
,3a≥3-3(
)
,
故a≥1-(
)
∴f'(1)=-3+b=3a-3,f(1)=b+c-2=1,
即有b=3a,c=-3a+3.
(2)由(1)可知f(x)=x3-3x2+3ax-3a+3,
x3-3x2+3ax-3a+3≥-
| 3 |
| 2 |
3ax-3a≥-x3+3x2-
| 9 |
| 2 |
3a(x-1)≥-x3+3x2-
| 9 |
| 2 |
当x=1时,成立,a∈R,
当x≠1时,3a≥
-x3+3x2-
| ||
| x-1 |
令t=x-1,3a≥
-t3+3t-
| ||
| t |
| ||
| t |
令g(t)=-t2+3-
| ||
| t |
∴以g′(t)=-2t+
| ||
| t2 |
-2t3+
| ||
| t2 |
| 5 |
| 4 |
| 1 |
| 3 |
| 5 |
| 4 |
| 1 |
| 3 |
g(t)max=g((
| 5 |
| 4 |
| 1 |
| 3 |
| 5 |
| 4 |
| 2 |
| 3 |
| 5 |
| 4 |
| 2 |
| 3 |
故a≥1-(
| 5 |
| 4 |
| 2 |
| 3 |
点评:本题主要考查导数在函数中的综合运用,利用切线求参数的值,利用导数求参数的取值范围,也就求最值问题,是一道综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
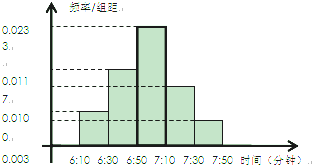 小明家订了一份报纸,寒假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示.
小明家订了一份报纸,寒假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示.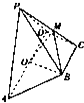 如图四棱锥P-ABCD的底面是一等腰梯形,其中AD∥BC,其中AD=3BC=6,AB=DC=2
如图四棱锥P-ABCD的底面是一等腰梯形,其中AD∥BC,其中AD=3BC=6,AB=DC=2