题目内容
已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ<
)的图象与x轴的交点中,相邻两个交点之间的距离为
,且图象上一个最低点为M(-
,-2).
(1)求f(x)的解析式;
(2)当x∈(0,
)时,求f(x)的值域.
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
(1)求f(x)的解析式;
(2)当x∈(0,
| π |
| 2 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)由题意可得半周期和A,求出周期,代入周期公式求得ω,最后代入最低点的坐标求解φ,则函数解析式可求;
(2)直接在函数解析式中由x的范围求得相位的范围,则函数的值域可求.
(2)直接在函数解析式中由x的范围求得相位的范围,则函数的值域可求.
解答:
解:(1)∵函数f(x)=Asin(ωx+φ)的图象与x轴的交点中,相邻两个交点之间的距离为
,且图象上一个最低点为M(-
,-2).
∴A=2,
=
,T=π,
则ω=2.
∴f(x)=2sin(2x+φ),
代入M(-
,-2),得-2=2sin[2×(-
)+φ],
即sin(φ-
)=-1.
∵0<φ<
,∴φ=
.
∴f(x)=2sin(2x+
);
(2)∵x∈(0,
),
∴2x+
∈(
,
),
则f(x)∈(-1,2].
| π |
| 2 |
| π |
| 3 |
∴A=2,
| T |
| 2 |
| π |
| 2 |
则ω=2.
∴f(x)=2sin(2x+φ),
代入M(-
| π |
| 3 |
| π |
| 3 |
即sin(φ-
| 2π |
| 3 |
∵0<φ<
| π |
| 2 |
| π |
| 6 |
∴f(x)=2sin(2x+
| π |
| 6 |
(2)∵x∈(0,
| π |
| 2 |
∴2x+
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
则f(x)∈(-1,2].
点评:本题考查了由y=Asin(ωx+φ)的部分图象求函数解析式,考查了三角函数的求值,是基础题.

练习册系列答案
相关题目
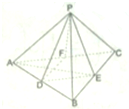 如图,在所有棱长都相等的正三棱锥P-ABC中,D,E,F分别是AB,BC,CA的中点,下列四个结论不成立的是( )
如图,在所有棱长都相等的正三棱锥P-ABC中,D,E,F分别是AB,BC,CA的中点,下列四个结论不成立的是( )| A、BC∥平面PDF |
| B、平面PDF⊥平面ABC |
| C、平面PAE⊥平面ABC |
| D、平面PDF⊥平面PAE |
要得到y=sinx的图象,只需先将y=sin(
x-
)的图象上所有点的纵坐标不变( )
| 1 |
| 2 |
| π |
| 6 |
A、横坐标缩短到原来的
| ||||
B、横坐标缩短到原来的
| ||||
C、横坐标伸长到原来的2倍,再将所得图象向左平移
| ||||
D、横坐标伸长到原来的2倍,再将所得图象向右平移
|
如图是某几何体的三视图,则该几何体的外接球的体积为( )


| A、8π | ||||
B、
| ||||
C、
| ||||
| D、64π |