Question

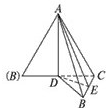如图，等边△ABC的边长为1，BC边上的高为AD，若沿AD折成直二面角，求二面角A-BC-D的正切值．

Answer 1

考点：二面角的平面角及求法

专题：空间角

分析：由题设知AD⊥平面BDC，作DE⊥BC于E，连AE，则AE⊥BC，所以∠AED是二面角A-BC-D的平面角，由此能求出二面角A-BC-D的正切值．

解答： 解：∵等边△ABC的边长为1，BC边上的高为AD，
∴AD⊥DB，AD⊥DC，
又DB∩DC=D，∴AD⊥平面BDC，
作DE⊥BC于E，连AE，则AE⊥BC，
∴∠AED是二面角A-BC-D的平面角，
等边△ABC的边长=1，∴它的高AD=

3

2

，
BD=DC=

1

2

，∠BDC=90°，∴BC=

2

2

，DE=

BC

2

=

2

4

，
∴tan∠AED=

AD

DE

=

3 2

2 4

=

6

，
∴二面角A-BC-D的正切值为

6

．

点评：本题考查二面角的正切值的求法，是基础题，解题时要认真审题，注意空间思维能力的求法．