题目内容

求定积分：
（1）
∫
2
1
x2-2x-3
x
dx；
（2）
∫
4
1
x
（1-
x
）dx．
考点：定积分
专题：导数的概念及应用
分析：根据定积分的计算法则计算即可．
解答： 解：（1）
∫
2
1
x2-2x-3
x
dx=
∫
2
1
（x-2-
3
x
）dx=（
1
2
x2-2x-3lnx）|
 
2
1
=-
1
2
-ln8；
（2）
∫
4
1
x
（1-
x
）dx=
∫
4
1
（
x
-x）dx=（
2
3
•x
3
2
-
1
2
x2）
|
4
1
=-
17
6
．
点评：本题考查了定积分的计算法则，属于基础题．
练习册系列答案
相关题目
对于实数m，n定义运算“⊕”：m⊕n=
-m2+2mn-1，m≤n
n2-mn，m＞n
，设f（x）=（2x-1）⊕（x-1），且关于x的方程f（x）=a恰有三个互不相等的实数根x1，x2，x3，则x1x2x3的取值范围是（　　）
A、（-
1
32
，0）
B、（-
1
16
，0）
C、（0，
1
32
）
D、（0，
1
16
）
已知函数f（x）=sin（2wx-
π
6
）-4sin2wx+2（w＞0），其图象与x轴相邻两个交点的距离为
π
2
．
（1）求函数f（x）的解析式；
（2）若将f（x）的图象向左平移m（m＞0）个长度单位得到函数g（x）的图象恰好经过点（-
π
3
，0），求当m取得最小值时，g（x）在[-
π
6
，
7π
12
]上的单调增区间．
一只昆虫随机飞落到一个边长为2的正方形区域内，则其落在正方形内切圆内的概率为
 
．
已知函数f（x）=
5
2
sinAsinx+cos2x（x∈R），其中A、B、C是△ABC的三个内角，且满足cos（A+
π
4
）=-
2
10
，A∈（
π
4
，
π
2
）
（1）求函数f（x）的值域；
（2）若f（x）max=f（B），且AC=5，求△ABC的面积．
已知
∫
e
0
xdx=
e2
2
，
∫
e
0
x3dx=
e4
4
，求下列定积分：
（1）
∫
e
0
（2x+x3）dx；
（2）
∫
e
0
（2x3-x+1）dx．
若P是长度为6的线段AB上任意一点，则点P到线段AB两端距离均不小于1的概率（　　）
A、
5
6
B、
2
3
C、
1
2
D、
1
3
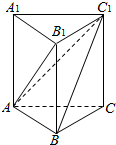如图，在三棱柱ABC-A1B1C1中，AA1⊥平面ABC，四边形A1ACC1是边长为2的正方形，AB=BC=
2
．
（1）求证：BC⊥AB1；
（2）求三棱锥 B1-ABC1的体积．
已知质点M按规律s=2t2+3做直线运动（位移单位：cm，时间单位：s）．
（1）当t=2，△t=0.01时，求
△s
△t
；   
（2））当t=2，△t=0.001时，求
△s
△t
；   
（3）当质点M在t=2时的瞬时速度．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网