题目内容
设偶函数f(x)在[0,+∞)为减函数,则不等式f(x)>f(2x+1)的解集是 .
考点:奇偶性与单调性的综合
专题:综合题,函数的性质及应用
分析:由题意,根据单调性及偶函数的性质,直接将式f(x)>f(2x+1)转化为|x|<|2x+1|,解此绝对值不等式即可.
解答:
解:偶函数f(x)在[0,+∞)为减函数,则
f(x)>f(2x+1)可变为|x|<|2x+1|,
解得x>-
或x<-1,
故答案为:x>-
或x<-1.
f(x)>f(2x+1)可变为|x|<|2x+1|,
解得x>-
| 1 |
| 3 |
故答案为:x>-
| 1 |
| 3 |
点评:本题解答的重点是利用函数的性质将不等式转化为|x|<|2x+1|,单调性与偶函数结合时,常转化出绝对值不等式,这是此类题的一个常见的转化方式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知回归直线
=
x+
的
估计值为0.2,样本点的中心为(4,5),则回归直线方程为( )
 |
| y |
 |
| b |
 |
| a |
 |
| a |
| A、y=1.2x-0.2 |
| B、y=1.2x+0.2 |
| C、y=0.2x+1.2 |
| D、y=0.2x-0.2 |
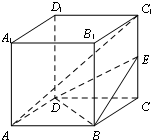 如图,在边长为2的正方体ABCD-A1B1C1D1中,E是棱CC1的中点.
如图,在边长为2的正方体ABCD-A1B1C1D1中,E是棱CC1的中点.