题目内容
函数f（x）=mx2+（m-3）x+1的图象与x 轴的交点至少有一个在原点右侧，则实数m的取值范围为 ．
考点：二次函数的性质
专题：计算题,函数的性质及应用
分析：函数图象与x轴的交点可化为方程的根，分类讨论．
解答：
解：①若m＜0，则方程mx2+（m-3）x+1=0有一正一负两个根，成立；
②若m=0，则-3x+1=0，成立；
③若m＞0，则f（0）=1＞0，-
＞0，△≥0，
解得0＜m≤1，
综上所述，m≤1．
故答案为：m≤1．
②若m=0，则-3x+1=0，成立；
③若m＞0，则f（0）=1＞0，-
| m-3 |
| 2m |
解得0＜m≤1，
综上所述，m≤1．
故答案为：m≤1．
点评：本题考查了函数的图象与x轴的交点与方程的根的关系，及分类讨论的数学思想，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
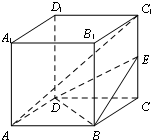如图，在边长为2的正方体ABCD-A1B1C1D1中，E是棱CC1的中点．
