题目内容
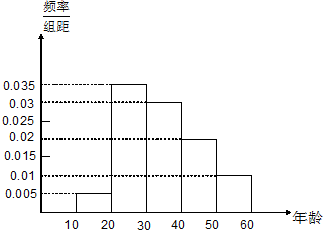某班同学利用寒假进行社会实践，对年龄段在[10，60]的人生活习惯是否符合环保理念进行调查，现随机抽取n人进行数据分析，得到如下频率分布表和频率分布直方图；（1）求出频率分布表中n，x，y的值；
（2）现从第三、四、五组中，采用分层抽样法抽取12人参加户外环保体验活动，则从这三组中应各抽取多少人？
（3）从第三、四、五组中采用分层抽样法抽取12人参加项学习活动，从这12名中再选取3人作为领队，记这3名领队中在第三四组内人数为X，求X分布列和期望EX．
| 组数 | 分组 | 人数 | 频率 |
| 第一组 | [10，20） | 5 | |
| 第二组 | [20，30） | x | |
| 第三组 | [30，40） | ||
| 第四组 | [40，50） | y | |
| 第五组 | [50，60] | ||
| 合计 | n |
考点：离散型随机变量的期望与方差,离散型随机变量及其分布列
专题：概率与统计
分析：（1）由频率分布表t 频率分布直方图，能求出频率分布表中n，x，y的值．
（2）先由频率分布图分求求出第三组的人数，第四组的人数和第五组的人数，再采用分层抽样法能求出从这三组中应各抽取多少人．
（3）由已知得X的可能取值为1，2，3，分别求出相应的概率，由此能求出X分布列和期望EX．
（2）先由频率分布图分求求出第三组的人数，第四组的人数和第五组的人数，再采用分层抽样法能求出从这三组中应各抽取多少人．
（3）由已知得X的可能取值为1，2，3，分别求出相应的概率，由此能求出X分布列和期望EX．
解答：
解：（1）由频率分布表得第1组的频率数为5，
由频率分布直方图得第1组的频率为0.005×10=0.05，
∴由题设条件可知：n=
=100，
x=0.035×10=0.35，
第四组的频率为0.02×10=0.2，
∴y=100×0.2=20．
（2）第三组的人数为0.03×10×100=30，
第四组的人数为0.02×10×100=20，
第五组的人数为0.01×10×100=10，
三组共计60人，从中抽取12人，
每组应抽取的人数为：
第三组
×12=6（人），
第四组
×12=2（人），
第五组
×12=2（人），
∴第3，4，5组分别抽取6人，4人，2人．
（3）由已知得X的可能取值为1，2，3，
P（X=1）=
=
，
P（X=2）=
=
，
P（X=3）=
=
，
∴X的分布列为：
EX=1×
+2×
+3×
=
．
由频率分布直方图得第1组的频率为0.005×10=0.05，
∴由题设条件可知：n=
| 5 |
| 0.05 |
x=0.035×10=0.35，
第四组的频率为0.02×10=0.2，
∴y=100×0.2=20．
（2）第三组的人数为0.03×10×100=30，
第四组的人数为0.02×10×100=20，
第五组的人数为0.01×10×100=10，
三组共计60人，从中抽取12人，
每组应抽取的人数为：
第三组
| 30 |
| 60 |
第四组
| 20 |
| 60 |
第五组
| 10 |
| 60 |
∴第3，4，5组分别抽取6人，4人，2人．
（3）由已知得X的可能取值为1，2，3，
P（X=1）=
| ||||
|
| 1 |
| 22 |
P（X=2）=
| ||||
|
| 9 |
| 22 |
P（X=3）=
| ||
|
| 6 |
| 11 |
∴X的分布列为：
| X | 1 | 2 | 3 | ||||||
| P |
|
|
|
| 1 |
| 22 |
| 9 |
| 22 |
| 6 |
| 11 |
| 85 |
| 22 |
点评：本题考查频率分布表和频率分布直方图的应用，考查分层抽样的应用，考查离散型随机变量的分布列和数学期望的求法，解题时要注意排列组合知识的合理运用．
练习册系列答案
相关题目