题目内容
10.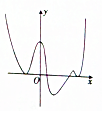 已知函数f′(x)的图象如图所示,其中f′(x)是f(x)的导函数,则f(x)的极值点的个数为( )
已知函数f′(x)的图象如图所示,其中f′(x)是f(x)的导函数,则f(x)的极值点的个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据极值点的定义和f′(x)的图象得出结论.
解答 解:若x0是f(x)的极值点,则f′(x0)=0,且f′(x)在x0两侧异号,
由f′(x)的图象可知f′(x)=0共有4解,
其中只有两个零点的左右两侧导数值异号,
故f(x)有2个极值点.
故选A.
点评 本题考查了极值点的定义,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
20.设复数z满足zi=1-2i,则z的虚部等于( )
| A. | -2i | B. | -i | C. | -1 | D. | -2 |
18.设f(x)是定义在R上的偶函数,对任意x∈R,都有f(x)=f(x+4),且当x∈[-2,0]时,$f(x)={(\frac{1}{2})^x}-1$,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有三个不同的实数根,则a的取值范围为( )
| A. | (1,2) | B. | (2,+∞) | C. | (1,$\root{3}{4}$) | D. | ($\root{3}{4}$,2) |
5.已知变量x,y满足条件$\left\{\begin{array}{l}x≥1\\ x-y≤0\\ x+2y-9≤0\end{array}\right.$则x+3y的最大值是( )
| A. | 4 | B. | 8 | C. | 12 | D. | 13 |
15.已知函数f(x)=$\frac{1}{2}$mcos2x+(m-2)sinx,其中1≤m≤2,若函数f(x)的最大值记为g(m),则g(m)的最小值为( )
| A. | -$\frac{1}{4}$ | B. | 1 | C. | 3-$\sqrt{3}$ | D. | $\sqrt{3}$-1 |
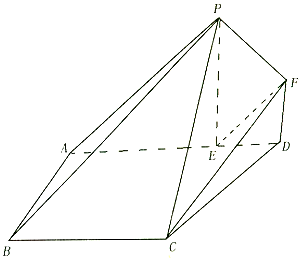 如图,在四边形ABCD中,∠BAD=90°,AD∥BC,PE⊥平面ABCD,E在AD上,FD∥PE,BC=AE=PE,DE=DF=$\frac{1}{2}$BC.
如图,在四边形ABCD中,∠BAD=90°,AD∥BC,PE⊥平面ABCD,E在AD上,FD∥PE,BC=AE=PE,DE=DF=$\frac{1}{2}$BC.