题目内容
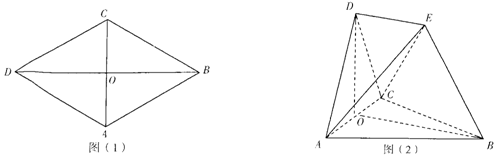
2.已知菱形ABCD如图(1)所示,其中∠ACD=60°,AB=2,AC与BD相交于点O,现沿AC进行翻折,使得平面ACD⊥平面ABC,取点E,连接AE,BE,CE,DE,使得线段BE再平面ABC内的投影落在线段OB上,得到的图形如图(2)所示,其中∠OBE=60°,BE=2.(Ⅰ)证明:DE⊥AC;
(Ⅱ)求多面体ABCDE的体积.
分析 (Ⅰ)推导出DO⊥AC,从而DO⊥平面ABC,作EF⊥平面ABC于F,由题意点F落在BO上,且∠EBF=∠OBE=60°,推导出DO∥EF,从而四边形DEFO是矩形,进而DE∥OF,由OF⊥AC,能证明DE⊥AC.
(Ⅱ)多面体ABCDE的体积VABCDE=2VA-BODE,由此能求出结果.
解答 证明:(Ⅰ)由图(1)知△ABC,△ACD都是边长为2的等边三角形,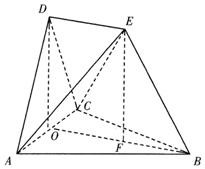
∴DO⊥AC,
又平面ACD⊥平面ABC,平面ACD∩平面ABC=AC,DO?平面ACD,
∴DO⊥平面ABC,
作EF⊥平面ABC于F,由题意点F落在BO上,
且∠EBF=∠OBE=60°,
在Rt△BEF中,EF=BE•sin∠EBF=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
在Rt△DOC中,DO=DC•sin∠DCO=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
∵DO⊥平面ABC,EF⊥平面ABC,∴DO∥EF,
又DO=EF,∴四边形DEFO是矩形,∴DE∥OF,
∵OF⊥AC,∴DE⊥AC.
解:(Ⅱ)依题意由(Ⅰ)可知:
多面体ABCDE的体积VABCDE=2VA-BODE=$2×\frac{1}{3}×\frac{(\sqrt{3}-1+\sqrt{3})×\sqrt{3}}{2}×1$=2-$\frac{\sqrt{3}}{3}$.
点评 本题考查线线垂直的证明,考查多面体体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、函数与方程思想、数形结合思想,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.某工程设备租赁公司为了调查A,B两种挖掘机的出租情况,现随机抽取了这两种挖掘机各100台,分别统计了每台挖掘机在一个星期内的出租天数,统计数据如下表:
A型车挖掘机
B型车挖掘机
(Ⅰ)根据这个星期的统计数据,将频率视为概率,求该公司一台A型挖掘机,一台B型挖掘机一周内合计出租天数恰好为4天的概率;
(Ⅱ)如果A,B两种挖掘机每台每天出租获得的利润相同,该公司需要从A,B两种挖掘机中购买一台,请你根据所学的统计知识,给出建议应该购买哪一种类型,并说明你的理由.
A型车挖掘机
| 出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 车辆数 | 5 | 10 | 30 | 35 | 15 | 3 | 2 |
| 出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 车辆数 | 14 | 20 | 20 | 16 | 15 | 10 | 5 |
(Ⅱ)如果A,B两种挖掘机每台每天出租获得的利润相同,该公司需要从A,B两种挖掘机中购买一台,请你根据所学的统计知识,给出建议应该购买哪一种类型,并说明你的理由.
13.已知F为双曲线C:$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1左焦点,过抛物线y2=20x的焦点的直线交双曲线C的右支于P,Q两点,若线段PQ的长等于双曲线C虚轴长的3倍,则△PQF的周长为( )
| A. | 40 | B. | 42 | C. | 44 | D. | 52 |
12.△ABC的三个内角A、B、C,所对的边分别是a、b、c,若a=2,c=2$\sqrt{3}$,tanA+tanB=$\sqrt{3}$-$\sqrt{3}$tanAtanB,则△ABC的面积S△ABC=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
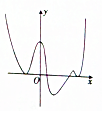 已知函数f′(x)的图象如图所示,其中f′(x)是f(x)的导函数,则f(x)的极值点的个数为( )
已知函数f′(x)的图象如图所示,其中f′(x)是f(x)的导函数,则f(x)的极值点的个数为( )