题目内容
19.已知不等式$\frac{|x+3|-1}{2}$>x的解集为(-∞,m).(Ⅰ)求实数m的值;
(Ⅱ)若关于x的方程|x-n|+|x+$\frac{1}{n}$|=m(n>0)有解,求实数n的值.
分析 (Ⅰ)根据x的范围得到关于x的不等式组,解出即可;(Ⅱ)根据绝对值不等式的性质得到关于n的不等式,解出即可.
解答 解:(Ⅰ)由题意得:$\frac{|x+3|-1}{2}$>x,
故|x+3|-2x-1>0,
故$\left\{\begin{array}{l}{x≤-3}\\{-(x+3)-2x-1>0}\end{array}\right.$或$\left\{\begin{array}{l}{x>-3}\\{x+3-2x-1>0}\end{array}\right.$,
解得:x<2,故m=2;
(Ⅱ)由题意得|x-n|+|x+$\frac{1}{n}$|=2有解,
∵|x-n|+|x+$\frac{1}{n}$|≥|(x-n)-(x+$\frac{1}{n}$)|=|n+$\frac{1}{n}$|=n+$\frac{1}{n}$≥2,
当且仅当n=1时”=“成立,
故n=1.
点评 本题考查了绝对值不等式的解法,不等式的性质,着重考查运算求解能力以及推理论证能力.

练习册系列答案
相关题目
4.要得到函数y=sin(2x+$\frac{π}{3}$)的图象,只需将函数y=cos2x的图象( )
| A. | 向左平移$\frac{π}{12}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{12}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
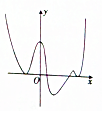 已知函数f′(x)的图象如图所示,其中f′(x)是f(x)的导函数,则f(x)的极值点的个数为( )
已知函数f′(x)的图象如图所示,其中f′(x)是f(x)的导函数,则f(x)的极值点的个数为( )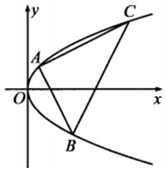 已知A、B、C是抛物线y2=2px(p>0)上三个不同的点,且AB⊥AC.
已知A、B、C是抛物线y2=2px(p>0)上三个不同的点,且AB⊥AC.