题目内容
已知F1，F2分别是双曲线
-y2=1（a＞0）的两个焦点，点P是双曲线上的一点，且满足∠F1PF2=90°，则△PF1F2的面积为（ ）
| x2 |
| a2 |
| A、4 | B、3 | C、2 | D、1 |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：由条件可得||PF1|-|PF2||=2a，由题意可知△F1PF2为直角三角形利用勾股定理，结合双曲线的定义，即可求出△PF1F2的面积．
解答：
解：由条件可得||PF1|-|PF2||=2a，由题意可知△F1PF2为直角三角形，
设双曲线的焦距为2c，则|PF1|2+|PF2|2=|F1F2|2=4c2，b2=1，
故（|PF1|-|PF2|）2+2|PF1|•|PF2|=|F1F2|2=4c2，即4a2+2|PF1|•|PF2|=4c2，
故|PF1|•|PF2|=2c2-2a2=2b2=2，
故△PF1F2的面积为
|PF1|•|PF2|=b2=1．
故选：D
设双曲线的焦距为2c，则|PF1|2+|PF2|2=|F1F2|2=4c2，b2=1，
故（|PF1|-|PF2|）2+2|PF1|•|PF2|=|F1F2|2=4c2，即4a2+2|PF1|•|PF2|=4c2，
故|PF1|•|PF2|=2c2-2a2=2b2=2，
故△PF1F2的面积为
| 1 |
| 2 |
故选：D
点评：本题考查双曲线的定义与性质，考查三角形面积的计算，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
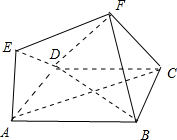如图所示，已知在多面体ABCDEF中，底面是正方形，EA⊥平面ABCD，EF∥AC且AC=2EF，AB=2AE=2
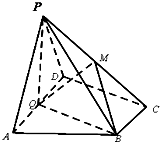如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，PA=PD=2，BC=
如图，在一个边长为2的正方形中随机撒入200粒的豆子，恰有120粒落在阴影区域里，则该阴影部分的面积约为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
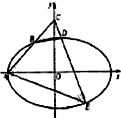已知B（-1，1）是椭圆