题目内容
已知关于t的一元二次方程t2+(2+i)t+2xy+(x-y)i=0(x,y∈R).当方程有实根时,则t的取值范围 .
考点:复数相等的充要条件,复数代数形式的混合运算
专题:数系的扩充和复数
分析:根据方程有实根,利用复数相等,建立条件关系即可得到结论.
解答:
解:设实根为t,则由t2+(2+i)t+2xy+(x-y)i=0得t2+2t+2xy+(t+x-y)i=0,
即
,消去参数t得(x-1)2+(y+1)2=2,
则所求点的轨迹为以(1,-1)为圆心,r=
的圆,
直线t=y-x与圆有公共点,则
≤
,
即|t+2|,解得-4≤t≤0,
故t的取值范围[-4,0],
故答案为:[-4,0]
即
|
则所求点的轨迹为以(1,-1)为圆心,r=
| 2 |
直线t=y-x与圆有公共点,则
| |1-(-1)+t| | ||
|
| 2 |
即|t+2|,解得-4≤t≤0,
故t的取值范围[-4,0],
故答案为:[-4,0]
点评:本题主要考查复数方程的求解,利用复数相等是解决本题的关键,涉及直线和圆的位置关系的应用.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
已知平面直角坐标系xOy内直线l的参数方程为
(t为参数),以Ox为极轴建立极坐标系(取相同的长度单位),圆C的极坐标方程为ρ=2
sin(θ+
),则直线l与圆C的公共点的个数为 .
|
| 2 |
| π |
| 4 |
在△ABC中,设命题p:
=
=
,命题q:△ABC是等边三角形,那么命题p是命题q的( )
| a |
| sinC |
| b |
| sinA |
| c |
| sinB |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若log0.5x>1,则x的取值范围是( )
A、(-∞,
| ||
B、(
| ||
C、(
| ||
D、(0,
|
某几何体的三视图如图所示,则该几何体的体积为( )


A、3+
| ||||
B、3+
| ||||
C、
| ||||
D、
|
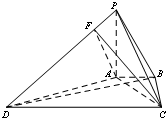 如图,在四棱锥P-ABCD中,已知AB=1,BC=2,CD=4,AB∥CD,BC⊥CD,平面PAB⊥平面ABCD,PA⊥AB.
如图,在四棱锥P-ABCD中,已知AB=1,BC=2,CD=4,AB∥CD,BC⊥CD,平面PAB⊥平面ABCD,PA⊥AB.