题目内容
设集合A为函数y=ln(-x2-2x+8)的定义域,集合B为函数y=x+
(x>-2)的值域,集合C为不等式(ax-1)(x-2)≤0的解集,(1)求A∩B;(2)若C⊆CRA,求a的取值范围.
| 1 |
| x+2 |
考点:集合的包含关系判断及应用,交集及其运算
专题:计算题,集合
分析:(1)通过对数函数的定义域求出集合A,函数的值域求出集合B,然后求解A与B的交集.
(2)求出A的补集,利用C⊆∁RA,通过a的范围,讨论不等式的解集,求出a的范围即可.
(2)求出A的补集,利用C⊆∁RA,通过a的范围,讨论不等式的解集,求出a的范围即可.
解答:
解:(1)∵-x2-2x+8>0,
∴解得A=(-4,2).
∵x>-2,∴y=x+
=x+2+
-2≥0.
∴B=[0,+∞);
∴A∩B=[0,2);
(2)∵CRA=(-∞,-4]∪[2,+∞),C⊆CRA,
若a<0,不等式(ax-1)(x-2)≤0的解集只能是(-∞,
]∪[2,+∞),故定有
≤-4得-
≤a<0.
若a>0,则不等式(ax-1)(x-2)≤0的解集只能是∅,否则不满足题意.
若a=0,不等式(ax-1)(x-2)≤0的解集只能是[2,+∞),满足题意,所以a=0成立.
∴a的范围为0≥a≥-
.
∴解得A=(-4,2).
∵x>-2,∴y=x+
| 1 |
| x+2 |
| 1 |
| x+2 |
∴B=[0,+∞);
∴A∩B=[0,2);
(2)∵CRA=(-∞,-4]∪[2,+∞),C⊆CRA,
若a<0,不等式(ax-1)(x-2)≤0的解集只能是(-∞,
| 1 |
| a |
| 1 |
| a |
| 1 |
| 4 |
若a>0,则不等式(ax-1)(x-2)≤0的解集只能是∅,否则不满足题意.
若a=0,不等式(ax-1)(x-2)≤0的解集只能是[2,+∞),满足题意,所以a=0成立.
∴a的范围为0≥a≥-
| 1 |
| 4 |
点评:本题主要考查了集合的交并补混合运算,较为简单,关键是将各集合的元素计算出来.考查分类讨论思想.

练习册系列答案
相关题目
已知“函数、数y=f(x)的图象关于点P(a,b)成中心对称图形”的充要条件为“函数y=f(x+a)-b是奇函数”,现有以下四个函数,
①y=
②y=(x-2)|x-2|+
x ③y=-
④y=log2
其中具有相同对称中心的两个函数的序号是( )
①y=
| 1-2x |
| x-4 |
| 1 |
| 2 |
| 8 |
| 2x+4 |
| 2x |
| 4-x |
其中具有相同对称中心的两个函数的序号是( )
| A、①和③ | B、①和④ |
| C、②和③ | D、②和④ |
下列有关命题的说法正确的是( )
| A、命题“若xy=0,则x=0”的否命题为:“若xy=0,则x≠0” |
| B、命题“若cosx=cosy,则x=y”的逆否命题为真命题 |
| C、若p∧q为假命题,则p,q均为假命题 |
| D、“若x+y=0,则x,y互为相反数”的逆命题为真命题 |
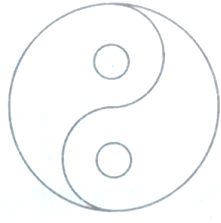 给如图所示的4个区域涂上颜色,可得一个漂亮的“太极图”,现有红、黑、黄、蓝四种颜色供选用,要求每个区域只能涂一种颜色,且相邻的区域颜色不同,则有
给如图所示的4个区域涂上颜色,可得一个漂亮的“太极图”,现有红、黑、黄、蓝四种颜色供选用,要求每个区域只能涂一种颜色,且相邻的区域颜色不同,则有