题目内容
已知f(x)为偶函数,且∫02f(x)dx=3,计算定积分∫-223f(x)dx.
考点:定积分,微积分基本定理
专题:导数的概念及应用
分析:根据定积分的几何意义知,定积分的值∫-223f(x)dx是f(x)的图象与x轴所围成的平面图形的面积的代数和,结合偶函数的图象的对称性即可解决问题.
解答:
解:∵f(x)为偶函数,且∫-20f(x)dx=∫02f(x)dx=3,
∴∫-223f(x)dx=3[∫-20f(x)dx+∫02f(x)]dx=3×(3+3)=18
∴∫-223f(x)dx=3[∫-20f(x)dx+∫02f(x)]dx=3×(3+3)=18
点评:本题主要考查定积分以及定积分的几何意义,属于基础题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
已知一个三棱锥的正视图和侧视图如图所示,则该三棱锥的俯视图可能为( )


A、 |
B、 |
C、 |
D、 |
设函数f(x)=kxm,若f(1)=1,f(
)=
,则不等式f(|x|)≤2的解集是( )
| 1 |
| 2 |
| ||
| 2 |
| A、{x|-4≤x≤4} | ||||
| B、{x|0≤x≤4} | ||||
C、{x|-
| ||||
D、{x|0<x≤
|
下列有关命题的说法正确的是( )
| A、命题“若xy=0,则x=0”的否命题为:“若xy=0,则x≠0” |
| B、命题“若cosx=cosy,则x=y”的逆否命题为真命题 |
| C、若p∧q为假命题,则p,q均为假命题 |
| D、“若x+y=0,则x,y互为相反数”的逆命题为真命题 |
设Sn是等差数列{an}的前n项和,S9=18,an-4=30(n>9),已知Sn=320,则n的值为( )
| A、10 | B、11 | C、20 | D、21 |
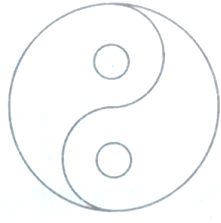 给如图所示的4个区域涂上颜色,可得一个漂亮的“太极图”,现有红、黑、黄、蓝四种颜色供选用,要求每个区域只能涂一种颜色,且相邻的区域颜色不同,则有
给如图所示的4个区域涂上颜色,可得一个漂亮的“太极图”,现有红、黑、黄、蓝四种颜色供选用,要求每个区域只能涂一种颜色,且相邻的区域颜色不同,则有