题目内容
已知△ABC中,A,B,C所对的边分别为a,b,c.
•
=m(m为正常数),∠BAC=θ,且a=2.
(Ⅰ)若bc有最大值4,求m的值及θ的取值范围;
(Ⅱ)在(Ⅰ)的条件下,求函数f(θ)=2cos2(θ+
)+2
sin2θ-
的最大值及相应的θ的值.
| AB |
| AC |
(Ⅰ)若bc有最大值4,求m的值及θ的取值范围;
(Ⅱ)在(Ⅰ)的条件下,求函数f(θ)=2cos2(θ+
| π |
| 4 |
| 3 |
| 3 |
考点:二倍角的余弦,平面向量数量积的运算,两角和与差的正弦函数,二倍角的正弦
专题:
分析:(1)向量的数量积,利用余弦定理求出b2+c2-2m=4,通过基本不等式求b•c的最大值及θ的取值范围;
(2)利用二倍角的余弦函数化简函数为一个角的三角函数的形式,通过角的范围正弦函数的最值求出函数的最大值即相应的θ值.
(2)利用二倍角的余弦函数化简函数为一个角的三角函数的形式,通过角的范围正弦函数的最值求出函数的最大值即相应的θ值.
解答:
解:(Ⅰ)由余弦定理可得,b2+c2-2bccosθ=4,即b2+c2-2m=4,又bc≤
(b2+c2)=m+2=4,∴m=2;
∴有bccosθ=2,cosθ=
≥
,∴θ∈(0,
];
(Ⅱ)∵f(θ)=1+cos(2θ+
)+
(1-cos2θ)-
=-sin2θ-
cos2θ+1
=-2sin(2θ+
)+1.
由(Ⅰ)可知θ∈(0,
],
∴2θ+
∈(
,π],sin(2θ+
)∈[0,1],
∴f(θ)max=1,此时θ=
.
| 1 |
| 2 |
∴有bccosθ=2,cosθ=
| 2 |
| bc |
| 1 |
| 2 |
| π |
| 3 |
(Ⅱ)∵f(θ)=1+cos(2θ+
| π |
| 2 |
| 3 |
| 3 |
| 3 |
=-2sin(2θ+
| π |
| 3 |
由(Ⅰ)可知θ∈(0,
| π |
| 3 |
∴2θ+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∴f(θ)max=1,此时θ=
| π |
| 3 |
点评:本题考查三角函数的化简求值,余弦定理的应用,掌握正弦函数的基本性质,是解好本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知向量
=(-1,2),
=(5,k),若
∥
,则实数k的值为( )
| a |
| b |
| a |
| b |
| A、5 | B、-5 | C、10 | D、-10 |
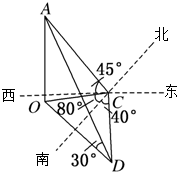 某人在C点测得某塔在南偏西80°的O处,塔顶A的仰角为45°,此人沿南偏东40°方向前进10米到D处,测得塔顶A的仰角为30°,求塔OA的高度?
某人在C点测得某塔在南偏西80°的O处,塔顶A的仰角为45°,此人沿南偏东40°方向前进10米到D处,测得塔顶A的仰角为30°,求塔OA的高度?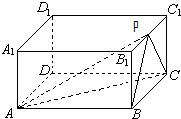 在正四棱柱ABCD-A1B1C1D1中,AB=2BB1=2,P为B1C1的中点.
在正四棱柱ABCD-A1B1C1D1中,AB=2BB1=2,P为B1C1的中点.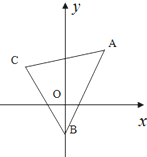 如图,已知三角形的顶点为A(2,4),B(0,-2),C(-2,3).求:
如图,已知三角形的顶点为A(2,4),B(0,-2),C(-2,3).求: