Question

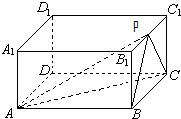在正四棱柱ABCD-A₁B₁C₁D₁中，AB=2BB₁=2，P为B₁C₁的中点．
（1）求直线AC与平面ABP所成的角；
（2）求异面直线AC与BP所成的角；
（3）求点B到平面APC的距离．

Answer 1

考点：异面直线及其所成的角,直线与平面所成的角

专题：空间位置关系与距离,空间角

分析：（1）建立如图所示的空间直角坐标系．A（2，0，0），C（0，2，0），B（2，2，0），P（1，2，1）．
设平面ABP的法向量为

m

=（x，y，z），则

m • AB =0 m • AP =0

，可得

m

．设直线AC与平面ABP所成的角为θ，则sinθ=|cosθ|=

| m • AC |

| m || AC |

即可得出．
（2）

BP

=（-1，0，1），利用cos＜

AC

，

BP

＞=

AC • BP

| AC || BP |

即可得出．
（3）设平面APC的法向量

n

=（x₀，y₀，z₀），利用

n • AP =0 n • AC =0

，可得

n

．再利用点B到平面APC的距离d=

| n • AB |

| n |

即可得出．

解答： 解：（1）建立如图所示的空间直角坐标系．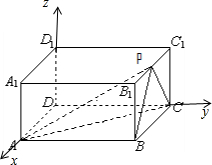
A（2，0，0），C（0，2，0），B（2，2，0），P（1，2，1）．

AC

=（-2，2，0），

AB

=（O，2，0），

AP

=（-1，2，1）．
设平面ABP的法向量为

m

=（x，y，z），
则

m • AB =0 m • AP =0

，化为

2y=0 -x+2y+z=0

，
令x=1，解得y=0，z=1．
∴

m

=（1，0，1）．
设直线AC与平面ABP所成的角为θ，则sinθ=|cosθ|=

| m • AC |

| m || AC |

=

2

2 • 8

=

1

2

，∴直线AC与平面ABP所成的角为30°．
（2）

BP

=（-1，0，1），∴cos＜

AC

，

BP

＞=

AC • BP

| AC || BP |

=

2

8 × 2

=

1

2

．
∴异面直线AC与BP所成的角为60°．
（3）设平面APC的法向量

n

=（x₀，y₀，z₀），
则

n • AP =0 n • AC =0

，∴

-x0+2y0+z0=0 -2x0+2y0=0

，令x₀=1，解得y₀=1，z₀=-1．
∴

n

=（1，1，-1）．
∴点B到平面APC的距离d=

| n • AB |

| n |

=

2

3

=

2 3

3

．

点评：本题考查了利用向量的夹角公式求空间角、数量积运算及法向量求空间距离，考查了推理能力与计算能力，属于难题．