Question

9．己知函数f（x）=4cosxsin（x+$\frac{π}{6}$）-1．
①求f（x）的最小正周期和单调区间；
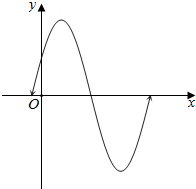
②用五点法作出其简图；
③求f（x）在区间[-$\frac{π}{6}$，$\frac{π}{4}$]上最大值和最小值．

Answer 1

分析 （1）利用和角公式展开，再利用二倍角公式与和角公式化简；
（2）列表，描点，作图；
（3）根据x的范围得出2x+$\frac{π}{6}$的范围，结合正弦函数性质得出f（x）的最值．

解答 解：①f（x）=2$\sqrt{3}$sinxcosx+2cos²x-1=$\sqrt{3}$sin2x+cos2x=2sin（2x+$\frac{π}{6}$）．
∴f（x）的最小正周期T=$\frac{2π}{2}$=π．
令-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{6}$≤$\frac{π}{2}$+2kπ．解得-$\frac{π}{3}$+kπ≤x≤$\frac{π}{6}$+kπ．
令$\frac{π}{2}$+2kπ≤2x+$\frac{π}{6}$≤$\frac{3π}{2}$+2kπ，解得$\frac{π}{6}$+kπ≤x≤$\frac{2π}{3}$+kπ．
∴f（x）的单调增区间是[-$\frac{π}{3}$+kπ，$\frac{π}{6}$+kπ]，减区间是[$\frac{π}{6}$+kπ，$\frac{2π}{3}$+kπ]，k∈Z．
②列表：

2x+$\frac{π}{6}$	0	$\frac{π}{2}$	π	$\frac{3π}{2}$	2π
x	-$\frac{π}{12}$	$\frac{π}{6}$	$\frac{5π}{12}$	$\frac{2π}{3}$	$\frac{11π}{12}$
2sin（2x+$\frac{π}{6}$）	0	2	0	-2	0

作出函数图象如图：

③∵x∈[-$\frac{π}{6}$，$\frac{π}{4}$]，∴2x+$\frac{π}{6}$∈[-$\frac{π}{6}$，$\frac{2π}{3}$]，
∴当2x+$\frac{π}{6}$=-$\frac{π}{6}$时，f（x）取得最小值-1，当2x+$\frac{π}{6}$=$\frac{π}{2}$时，f（x）取得最大值2．

点评 本题考查了三角函数的恒等变换与化简求值，三角函数的性质，及五点法作图．属于中档题．