题目内容
已知△ABC中,AB=
,AC=1,∠B=30°.求:
(1)△ABC的面积;
(2)△ABC的周长.
| 3 |
(1)△ABC的面积;
(2)△ABC的周长.
考点:正弦定理,余弦定理
专题:解三角形
分析:(1)由条件利用正弦定理求得sinC的值,可得C的值,利用三角形内角和公式求得A,再根据,△ABC的面积为
AB•AC•sinA,计算求得结果.
(2)由条件求得BC的值,可得,△ABC的周长为AB+AC+BC的值.
| 1 |
| 2 |
(2)由条件求得BC的值,可得,△ABC的周长为AB+AC+BC的值.
解答:
解:(1)△ABC中,∵AB=
,AC=1,∠B=30°,由正弦定理可得
=
,
即
=
,求得sinC=
,∴C=60°,或C=120°.
当C=60°时,A=90°,△ABC的面积为
AB•AC=
;当C=120°时,A=30°,△ABC的面积为
AB•AC•sinA=
.
(2)当C=60°时,A=90°,BC=
=2,△ABC的周长为AB+AC+BC=
+1+2=3+
.
当C=120°时,A=30°=B,BC=AC=1,△ABC的周长为AB+AC+BC=
+1+1=2+
.
| 3 |
| AB |
| sinC |
| AC |
| sinB |
即
| ||
| sinC |
| 1 |
| sin30° |
| ||
| 2 |
当C=60°时,A=90°,△ABC的面积为
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
(2)当C=60°时,A=90°,BC=
| AB2+AC2 |
| 3 |
| 3 |
当C=120°时,A=30°=B,BC=AC=1,△ABC的周长为AB+AC+BC=
| 3 |
| 3 |
点评:本题主要考查正弦定理和余弦定理的应用,三角形内角和公式,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
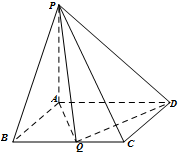 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=tBC(t>0)
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=tBC(t>0)