题目内容
若a,b都是实数,则“a-b>0”是“a2-b2>0”的( )
| A、既不充分也不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、充分而不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:由a-b>0得,a>b;由a2-b2>0得,a2>b2,所以容易判断由a-b>0能否得到a2-b2>0,而由a2-b2>0能否得到a-b>0,所以就可以判断a-b>0是a2-b2>0的什么条件了.
解答:
解:由a-b>0得,a>b;由a2-b2>0得a2>b2;
而由a>b,得不到a2>b2,比如1>-2,得不到12>(-2)2,即a-b>0不是a2-b2>0的充分条件;
而由a2>b2得不到a>b,比如(-3)2>12,得不到-3>1,即a-b不是a2-b2>0的必要条件;
∴a-b>0是a2-b2>0的既不充分又不必要条件.
故选A.
而由a>b,得不到a2>b2,比如1>-2,得不到12>(-2)2,即a-b>0不是a2-b2>0的充分条件;
而由a2>b2得不到a>b,比如(-3)2>12,得不到-3>1,即a-b不是a2-b2>0的必要条件;
∴a-b>0是a2-b2>0的既不充分又不必要条件.
故选A.
点评:考查不等式两边同时平方所得不等式方向有何变化,而对于a2>b2,去掉平方号之后a,b有何关系,以及充分条件,必要条件,既不充分也不必要条件的概念.

练习册系列答案
相关题目
下列各式中,最小值等于2的是( )
| A、logab+logba | ||||
B、
| ||||
C、tanθ+
| ||||
| D、2x+2-x |
等差数列{an}的前n项和为Sn,已知(a2-1)3+2012(a2-1)=sin
,(a2012-1)3+2012(a2012-1)=cos
,则S2013等于( )
| 2011π |
| 3 |
| 2011π |
| 6 |
| A、2013 | ||
| B、4026 | ||
| C、0 | ||
D、2013
|
已知两点A(4,1),B(7,-3),则向量
的模等于( )
| AB |
| A、5 | ||
B、
| ||
C、3
| ||
D、
|
已知A,B,C三点共线,且直线AB不过点O,
=m
+n
,则m2+n的最小值为( )
| OC |
| OA |
| OB |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
i是虚数单位,则1+i+i2+i3=( )
| A、1 | B、i | C、1-i | D、0 |
不等式2x2>3x-1的解集为( )
| A、∅ | ||
B、{x|x<-
| ||
C、(-∞,
| ||
D、{
|
已知函数f(x)=
,则f(f(
))的值是( )
|
| 1 |
| 2 |
| A、2 | ||
B、
| ||
| C、1 | ||
| D、4 |
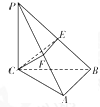 如图,已知三棱锥P-ABC中,PC⊥平面ABC,AB⊥BC,PC=BC=4,AB=2,E、F分别是PB、PA的中点.
如图,已知三棱锥P-ABC中,PC⊥平面ABC,AB⊥BC,PC=BC=4,AB=2,E、F分别是PB、PA的中点.