题目内容
甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头,它们在一昼夜内任何时刻到达是等可能的.
(1)如果甲船和乙船的停泊时间都是4小时,求它们中的任何一条船不需要等待码头空出的概率;
(2)如果甲船的停泊时间为4小时,乙船的停泊时间是6小时,求它们中的任何一条船需要等待码头空出的概率.
(1)如果甲船和乙船的停泊时间都是4小时,求它们中的任何一条船不需要等待码头空出的概率;
(2)如果甲船的停泊时间为4小时,乙船的停泊时间是6小时,求它们中的任何一条船需要等待码头空出的概率.
考点:几何概型
专题:应用题,概率与统计
分析:(1)如果甲船和乙船的停泊时间都是4小时,设甲、乙两船到达时间分别为x、y,我们可以画出(x,y)点对称的平面区域,及满足条件y-x>4或y-x<-4平面区域,分别求出对应面积,代入几何概型公式,即可求出答案.
(2)如果甲船的停泊时间为4小时,乙船的停泊时间是6小时,求出满足条件|y-x|>4或|y-x|>2对应的平面区域的面积,代入几何概型公式,即可求出答案.
(2)如果甲船的停泊时间为4小时,乙船的停泊时间是6小时,求出满足条件|y-x|>4或|y-x|>2对应的平面区域的面积,代入几何概型公式,即可求出答案.
解答:
解:(1)设甲、乙两船到达时间分别为x、y,则O≤x<24,0≤y<24且y-x>4或y-x<-4
作出区域
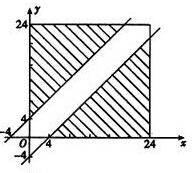
设“两船无需等待码头空出”为事件A,则P(A)=
=
.
(2)当甲船的停泊时间为4小时,两船不需等待码头空出,则满足|x-y|>2.设在上述条件时“两船不需等待码头空出”为事件B,画出区域.
,
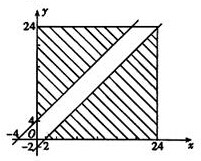
P(B)=
=
.
作出区域
|

设“两船无需等待码头空出”为事件A,则P(A)=
2×
| ||
| 24×24 |
| 25 |
| 36 |
(2)当甲船的停泊时间为4小时,两船不需等待码头空出,则满足|x-y|>2.设在上述条件时“两船不需等待码头空出”为事件B,画出区域.
|

P(B)=
| ||||
| 24×24 |
| 221 |
| 288 |
点评:本题考查的知识点是几何概型,其中求出所有基本事件对应的平面区域的面积,及满足条件 的平面区域的面积是解答本题的关键.

练习册系列答案
相关题目
等差数列{an}的前n项和为Sn,已知(a2-1)3+2012(a2-1)=sin
,(a2012-1)3+2012(a2012-1)=cos
,则S2013等于( )
| 2011π |
| 3 |
| 2011π |
| 6 |
| A、2013 | ||
| B、4026 | ||
| C、0 | ||
D、2013
|
不等式2x2>3x-1的解集为( )
| A、∅ | ||
B、{x|x<-
| ||
C、(-∞,
| ||
D、{
|
已知函数f(x)=
,则f(f(
))的值是( )
|
| 1 |
| 2 |
| A、2 | ||
B、
| ||
| C、1 | ||
| D、4 |
下列说法中正确的是( )
| A、数列{lg2n}是等差数列而不是等比数列 |
| B、公比q>1的等比数列中各项都大于1 |
| C、公比q<0的等比数列是递减数列 |
| D、常数列是公比为1的等比数列 |
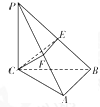 如图,已知三棱锥P-ABC中,PC⊥平面ABC,AB⊥BC,PC=BC=4,AB=2,E、F分别是PB、PA的中点.
如图,已知三棱锥P-ABC中,PC⊥平面ABC,AB⊥BC,PC=BC=4,AB=2,E、F分别是PB、PA的中点.