题目内容
5.在直角坐标系中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=4cosθ-2sinθ,直线l的极坐标方程为2aρcosθ+2ρsinθ=1(a为常数).(1)求直线l与圆C的普通方程;
(2)若直线l分圆C所得两弧长度之比为1:2,求实数a的值.
分析 (1)由ρ2=x2+y2,ρcosθ=x,ρsinθ=y,能求出直线l的普通方程和圆C的普通方程.
(2)由直线l分圆C所得两弧长度之比为1:2,得到圆心C(2,-1)到直线2ax+2y-1=0的距离为半径一半,由此能求出a.
解答 解:(1)∵直线l的极坐标方程为2aρcosθ+2ρsinθ=1(a为常数),
∴直线l的普通方程为2ax+2y-1=0.
∵圆C的极坐标方程为ρ=4cosθ-2sinθ,
∴ρ2=4ρcosθ-2ρsinθ,
∴圆C的普通方程为:x2+y2-4x+2y=0.
(2)∵圆C:x2+y2-4x+2y=0的圆心C(2,-1),半径r=$\frac{1}{2}\sqrt{16+4}$=$\sqrt{5}$,
直线l分圆C所得两弧长度之比为1:2,
∴直线l截圆C所得的弦|AB|所对圆心角为120°,
∴圆心C(2,-1)到直线2ax+2y-1=0的距离为半径一半,
即d=$\frac{|4a-2-1|}{\sqrt{4{a}^{2}+4}}$=$\frac{\sqrt{5}}{2}$,解得a=$\frac{2}{11}$或a=2.
点评 本题考查直线与圆的普通方程的求法,是中档题,解题时要认真审题,注意极坐标与直角坐标互化公式的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.已知钝角α满足cosα=-$\frac{1}{3}$,则sin$\frac{α}{2}$等于( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{1}{6}$ |
4. 已知正四棱锥的底面边长为2a,其侧视图是腰长为2的等腰三角形(如图所示),当正视图的面积最大时,该正四棱锥的表面积为( )
已知正四棱锥的底面边长为2a,其侧视图是腰长为2的等腰三角形(如图所示),当正视图的面积最大时,该正四棱锥的表面积为( )
 已知正四棱锥的底面边长为2a,其侧视图是腰长为2的等腰三角形(如图所示),当正视图的面积最大时,该正四棱锥的表面积为( )
已知正四棱锥的底面边长为2a,其侧视图是腰长为2的等腰三角形(如图所示),当正视图的面积最大时,该正四棱锥的表面积为( )| A. | 8 | B. | 8+8$\sqrt{2}$ | C. | 8$\sqrt{2}$ | D. | 4+8$\sqrt{2}$ |
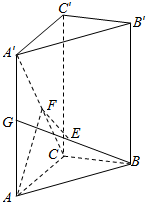 已知直三棱柱ABC-A′B′C′中,∠ACB=90°,BE=GE,AG=A′G,F是线段A′C上的点,EF∥平面ACB.
已知直三棱柱ABC-A′B′C′中,∠ACB=90°,BE=GE,AG=A′G,F是线段A′C上的点,EF∥平面ACB.