题目内容
在平面直角坐标系中,对于函数y=f(x)的图象上不重合的两点A,B,若A,B关于原点对称,则称点对(A,B)是函数y=f(x)的一组“奇点对”(规定(A,B)与(B,A)是相同的“奇点对”).函数f(x)=
的“奇点对”的组数是 .
|
考点:分段函数的应用
专题:函数的性质及应用
分析:根据“奇点对”的定义可知,只需要利用图象,作出函数f(x)=-x+4,x>0关于原点对称的图象,利用对称图象在x<0上两个图象的交点个数,即为“奇点对”的个数.
解答:
 解:由题意知函数f(x)=-x+4,x>0关于原点对称的图象为-y=x+4,
解:由题意知函数f(x)=-x+4,x>0关于原点对称的图象为-y=x+4,
即y=-x-4,x<0
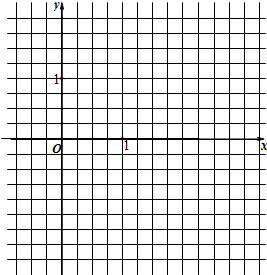
在x<0上作出两个函数的图象如图,
由图象可知两个函数在x<0上的交点个数有2个,
∴函数f(x)的“奇点对”有2组,
故答案为:2.
 解:由题意知函数f(x)=-x+4,x>0关于原点对称的图象为-y=x+4,
解:由题意知函数f(x)=-x+4,x>0关于原点对称的图象为-y=x+4,即y=-x-4,x<0
在x<0上作出两个函数的图象如图,
由图象可知两个函数在x<0上的交点个数有2个,
∴函数f(x)的“奇点对”有2组,
故答案为:2.
点评:本题主要考查新定义题目,读懂题意,利用数形结合的思想是解决本题的关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
如图是计算
+
+
+
+
值的一个程序框图,其中判断框内应填入的条件是( )
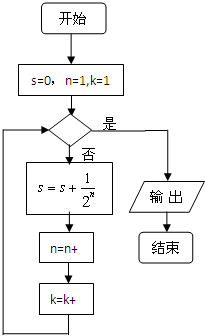
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |

| A、K>5? | B、K<5? |
| C、K>10? | D、K<10? |
阅读程序框图,若输入m=1,n=2,则输出n=( )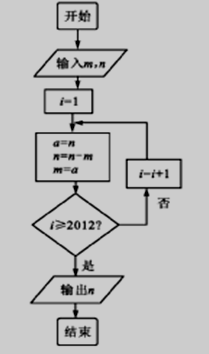

| A、1 | B、-1 | C、2 | D、-2 |
已知
=(-2,0),
=(0,2)(O为坐标原点),点C在曲线
(θ为参数)上运动,则△ABC面积的最大值为( )
| OA |
| OB |
|
A、3-
| ||||
B、3+
| ||||
C、
| ||||
D、
|
执行如图程序框图,那么输出S的值为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
设2x=5y=m,且
+
=2,则m的值是( )
| 1 |
| x |
| 1 |
| y |
A、±
| ||
B、
| ||
| C、10 | ||
| D、100 |
已知点P(x,y)的坐标满足条件:
,则
x+y的最小值为( )
|
| 3 |
A、
| ||
| B、0 | ||
C、-
| ||
D、-
|
已知向量
=(-1,2),
=(2,x),
=(x,-3),若
∥
,则|
|等于( )
| a |
| b |
| c |
| a |
| b |
| c |
A、
| ||
| B、10 | ||
C、
| ||
| D、5 |
 已知函数
已知函数