题目内容
一个四棱锥的三视图如图所示,那么对于这个四棱锥,下列说法中正确的是( ) 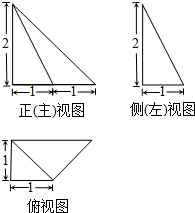

A、最长棱的棱长为
| ||
| B、最长棱的棱长为3 | ||
| C、侧面四个三角形中有且仅有一个是正三角形 | ||
| D、侧面四个三角形都是直角三角形 |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由三视图可知:该几何体如图所示,PA⊥底面ABCD,PA=2,底面是一个直角梯形,其中BC∥AD,AB⊥AD,BC=AB=1,AD=2.可得△PAD,△PAB,△PBC是直角三角形.
再利用三垂线定理可得△PCD是直角三角形.即可得出.
再利用三垂线定理可得△PCD是直角三角形.即可得出.
解答:
解:由三视图可知:该几何体如图所示,PA⊥底面ABCD,PA=2,底面是一个直角梯形,其中BC∥AD,AB⊥AD,BC=AB=1,AD=2.
可得△PAD,△PAB,△PBC是直角三角形.
取AD的中点O,连接OC,AC.
可得四边形ABCO是平行四边形,∴OC=OD=OA=1,
∴CD⊥AC,
∵PA⊥底面ABCD,
∴CD⊥PC,
因此△PCD是直角三角形.
综上可得:四棱锥的侧面四个三角形都是直角三角形.
故选:D.

可得△PAD,△PAB,△PBC是直角三角形.
取AD的中点O,连接OC,AC.
可得四边形ABCO是平行四边形,∴OC=OD=OA=1,
∴CD⊥AC,
∵PA⊥底面ABCD,
∴CD⊥PC,
因此△PCD是直角三角形.
综上可得:四棱锥的侧面四个三角形都是直角三角形.
故选:D.
点评:本题考查了线面垂直的判定与性质定理、三垂线定理的应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
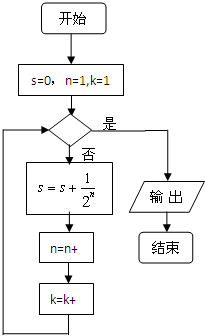
如图是计算
+
+
+
+
值的一个程序框图,其中判断框内应填入的条件是( )
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |

| A、K>5? | B、K<5? |
| C、K>10? | D、K<10? |
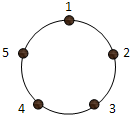 如图,圆周上按顺时针方向标有1,2,3,4,5五个点,一只青蛙按瞬时针方向绕圆从一个点跳到下一个点.若它停在奇数点上,则下一次只能跳一个点,若停在偶数点上,则可以连续跳2个点.该青蛙从5这点起跳,经2009次跳后它将停在的点是( )
如图,圆周上按顺时针方向标有1,2,3,4,5五个点,一只青蛙按瞬时针方向绕圆从一个点跳到下一个点.若它停在奇数点上,则下一次只能跳一个点,若停在偶数点上,则可以连续跳2个点.该青蛙从5这点起跳,经2009次跳后它将停在的点是( )| A、1 | B、2 | C、3 | D、4 |
某小学教师准备购买一些签字笔和铅笔盒作为奖品,已知签字笔每支5元,铅笔盒每个6元,花费总额不能超过50元.为了便于学生选择,购买签字笔和铅笔盒的个数均不能少于3个,那么该教师有 种不同的购买奖品方案.
阅读程序框图,若输入m=1,n=2,则输出n=( )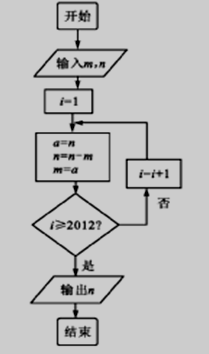

| A、1 | B、-1 | C、2 | D、-2 |
已知
=(-2,0),
=(0,2)(O为坐标原点),点C在曲线
(θ为参数)上运动,则△ABC面积的最大值为( )
| OA |
| OB |
|
A、3-
| ||||
B、3+
| ||||
C、
| ||||
D、
|
 已知函数
已知函数