题目内容
已知函数f(x)=2sin2xcos2
+cos2xsinφ-sin2x(0<φ<π)图象的一条对称轴为x=
.
(Ⅰ)求φ的值;
(Ⅱ)若存在x0∈[-
,
]使得|f(x0)-m|≤
成立,求实数m的取值范围;
(Ⅲ)已知函数g(x)=|f(
-
)|+|cosωx|在区间[0,1]上恰有50次取到最大值,求正数ω的取值范围.
| φ |
| 2 |
| π |
| 3 |
(Ⅰ)求φ的值;
(Ⅱ)若存在x0∈[-
| π |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
(Ⅲ)已知函数g(x)=|f(
| ωx |
| 2 |
| 5π |
| 12 |
考点:三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:(Ⅰ)奇函数f(x)进行化简,利用函数的对称轴,建立方程关系,即可求φ的值;
(Ⅱ)将不等式|f(x0)-m|≤
进行转化,求出不等式的等价条件,即可求实数m的取值范围;
(Ⅲ)将函数g(x)进行化简,根据三角函数的图象和性质,求出函数的周期,即可得到结论.
(Ⅱ)将不等式|f(x0)-m|≤
| 1 |
| 2 |
(Ⅲ)将函数g(x)进行化简,根据三角函数的图象和性质,求出函数的周期,即可得到结论.
解答:
解:(Ⅰ)Ⅰ)f(x)=2sin2xcos2
+cos2xsinφ-sin2x=sin(2x+φ),
∵0<φ<π,图象的一条对称轴为x=
,
∴2×
+φ=kπ+
,解得φ=kπ-
,
∵0<φ<π,
∴当k=1时,φ=π-
=
.
即f(x)=sin(2x+
).
(II)由|f(x0)-m|≤
得-
≤f(x0)-m≤
,即f(x0)-
≤m≤f(x0)+
,
∵x0∈[-
,
],∴
≤2x0+
≤
,
即-
≤sinx(2x0+
)≤1,
∴若存在x0∈[-
,
]使得|f(x0)-m|≤
成立,
则-1≤m≤
.
(III)g(x)=|f(
-
)|+|cosωx|=|sinωx|+|cosωx|=
=
,
若g(x)取得最大值,则|sin2ωx|=1,等价于y=|sin2ωx|在[0,1]上恰有50次取到最大值1,
由y=|sin2ωx|的最小正周期T=
,
由此可得49•
+
≤1<50•
+
,
解得
≤ω<
.
| φ |
| 2 |
∵0<φ<π,图象的一条对称轴为x=
| π |
| 3 |
∴2×
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
∵0<φ<π,
∴当k=1时,φ=π-
| π |
| 6 |
| 5π |
| 6 |
即f(x)=sin(2x+
| 5π |
| 6 |
(II)由|f(x0)-m|≤
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵x0∈[-
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| 7π |
| 6 |
即-
| 1 |
| 2 |
| 5π |
| 6 |
∴若存在x0∈[-
| π |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
则-1≤m≤
| 3 |
| 2 |
(III)g(x)=|f(
| ωx |
| 2 |
| 5π |
| 12 |
| (|sinωx|+|cosωx|)2 |
| 1+|sin2ωx| |
若g(x)取得最大值,则|sin2ωx|=1,等价于y=|sin2ωx|在[0,1]上恰有50次取到最大值1,
由y=|sin2ωx|的最小正周期T=
| π |
| 2ω |
由此可得49•
| π |
| 2ω |
| π |
| 4ω |
| π |
| 2ω |
| π |
| 4ω |
解得
| 99π |
| 4 |
| 101π |
| 4 |
点评:本题主要考查三角函数的图象和性质,利用三角函数的关系式进行化简是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
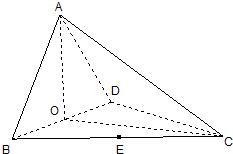 如图,四面体ABCD中,O、E分别是BD、BC的中点,AB=AD=
如图,四面体ABCD中,O、E分别是BD、BC的中点,AB=AD= 下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.