Question

17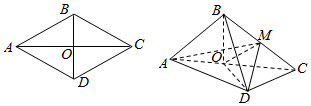．如图，菱形ABCD的边长为6，∠BAD=60°，AC∩BD=O，将菱形ABCD沿对角线AC折起得三棱锥，点M是棱BC的中点，DM=3$\sqrt{2}$．
（1）求证：平面ABC⊥平面MDO；
（2）求三棱锥M-ABD的体积．

Answer 1

分析 （1）由菱形的性质计算OM，OD，根据勾股定理得逆定理得出OD⊥OM，又OD⊥AC，故OD⊥平面ABC，于是平面ABC⊥平面MDO；
（2）V_M-ABD=V_D-ABM．代入棱锥的体积公式计算即可．

解答 解：（1）∵四边形ABCD是菱形，∠BAD=60°，
∴OD⊥AC，OB⊥OC，BD=AB=6，
∵M是BC的中点，
∴OM=$\frac{1}{2}BC$=3，OD=3，
∵DM=3$\sqrt{2}$，
∴OD²+OM²=DM²，
∴OD⊥OM，
∵OM?平面ABC，AC?平面ABC，OM∩AC=O，
∴OD⊥平面ABC，∵OD?平面MDO，
∴平面ODM⊥平面ABC．
（2）由（Ⅰ）知 OD⊥平面ABC，且OD=3，
∴V_M-ABD=V_D-ABM=$\frac{1}{3}$S_△ABM•OD=$\frac{1}{3}×\frac{1}{2}$AB•BM•sin∠ABM•OD
=$\frac{1}{3}×\frac{1}{2}×6×3×\frac{\sqrt{3}}{2}×3$
=$\frac{9\sqrt{3}}{2}$．

点评 本题考查了面面垂直的判定，线面垂直的判定，棱锥的体积计算，属于中档题．