题目内容
7.在△ABC中,D为边BC上一点,CD=2BD,∠ADB=120°,AD=2,且△ADC的面积为$\sqrt{3}$.(Ⅰ)求sinB的值;
(Ⅱ)求cos(2B-$\frac{π}{3}$)的值.
分析 (Ⅰ)由已知可求∠ADC=60°,利用三角形面积公式可求DC,由已知可求BD,由余弦定理可求AB的值,利用正弦定理即可解得sinB的值.
(Ⅱ)由题意利用同角三角函数基本关系式可求cosB,利用倍角公式可求sin2B,cos2B的值,根据两角差的余弦函数公式即可计算得解cos(2B-$\frac{π}{3}$)的值.
解答 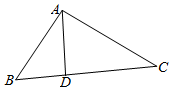 (本题满分为13分)
(本题满分为13分)
解:(Ⅰ)∵∠ADB=120°,∴∠ADC=60°.
∵AD=2,
∴由S△ADC=$\frac{1}{2}$AD•DC•sin∠ADC=$\sqrt{3}$,得DC=2,…(3分)
∵BD=$\frac{1}{2}$DC,∴BD=1,BC=3.
在△ABD中,由余弦定理得AB2=AD2+BD2-2AD•BDcos∠ADB=7,
∴AB=$\sqrt{7}$,
由正弦定理得$\frac{AD}{sinB}$=$\frac{AB}{sin∠ADB}$,∴sinB=$\frac{{\sqrt{21}}}{7}$. …(7分)
(Ⅱ)∵sinB=$\frac{{\sqrt{21}}}{7}$,且B为锐角,∴cosB=$\frac{{2\sqrt{7}}}{7}$,
∴sin2B=2sinBcosB=$\frac{{4\sqrt{3}}}{7}$,cos2B=2cos2B-1=$\frac{1}{7}$,…(11分)
∴cos(2B-$\frac{π}{3}$)=$\frac{1}{2}$cos2B+$\frac{{\sqrt{3}}}{2}$sin2B=$\frac{13}{14}$.…(13分)
点评 本题主要考查了三角形面积公式,余弦定理,正弦定理,同角三角函数基本关系式,倍角公式以及两角差的余弦函数公式在解三角形中的应用,考查了计算能力和转化思想,属于中档题.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案| A. | 1-2i | B. | -$\frac{11}{5}$+2i | C. | 1+2i | D. | -4+2i |
| A. | -3 | B. | 3 | C. | -3或3 | D. | -1或3 |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | (2,+∞) | B. | (1,2) | C. | (0,2) | D. | [1,2] |
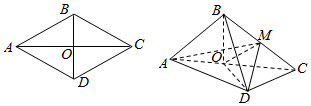 如图,菱形ABCD的边长为6,∠BAD=60°,AC∩BD=O,将菱形ABCD沿对角线AC折起得三棱锥,点M是棱BC的中点,DM=3$\sqrt{2}$.
如图,菱形ABCD的边长为6,∠BAD=60°,AC∩BD=O,将菱形ABCD沿对角线AC折起得三棱锥,点M是棱BC的中点,DM=3$\sqrt{2}$.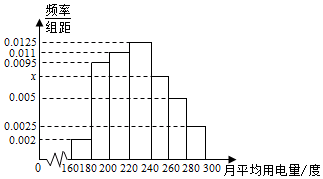 某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.
某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.