题目内容
12.已知双曲线${C_1}:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的离心率为2,则双曲线${C_2}:\frac{x^2}{b^2}-\frac{y^2}{a^2}=1$的离心率为$\frac{2\sqrt{3}}{3}$.分析 由题意可得c=2a,由a,b,c的关系可得b=$\sqrt{3}$a,由双曲线C2的离心率为$\frac{c}{b}$,计算即可得到所求值.
解答 解:由题意可得e=$\frac{c}{a}$=2,
即c=2a,
由c2=a2+b2,可得b2=3a2,
可得双曲线C2的离心率为$\frac{c}{b}$=$\sqrt{\frac{{a}^{2}+{b}^{2}}{{b}^{2}}}$
=$\sqrt{1+\frac{{a}^{2}}{{b}^{2}}}$=$\sqrt{1+\frac{1}{3}}$=$\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题考查双曲线的离心率的求法,注意运用双曲线的a,b,c的关系,考查化简整理的运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左、右焦点分别为F1,F2.若左焦点F1关于其中一条渐近线的对称点位于双曲线上,则该双曲线的离心率e的值为( )
| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{5}$ | D. | 5 |
7.已知函数y=f(x)=|x-1|-mx,若关于x的不等式f(x)<0解集中的整数恰为3个,则实数m的取值范围为 ( )
| A. | $\frac{2}{3}<m≤\frac{3}{4}$ | B. | $\frac{3}{4}<m≤\frac{4}{5}$ | C. | $\frac{2}{3}<m<\frac{3}{4}$ | D. | $\frac{3}{4}<m<\frac{4}{5}$ |
2.i是虚数单位,满足(1+2i)z=-3+4i的复数z=( )
| A. | 1-2i | B. | -$\frac{11}{5}$+2i | C. | 1+2i | D. | -4+2i |
 已知长方形ABCD中,AB=3,AD=4,现将长方形沿对角线BD折起,使AC=a,得到一个四面体A-BCD,如图所示.
已知长方形ABCD中,AB=3,AD=4,现将长方形沿对角线BD折起,使AC=a,得到一个四面体A-BCD,如图所示.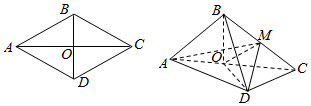 如图,菱形ABCD的边长为6,∠BAD=60°,AC∩BD=O,将菱形ABCD沿对角线AC折起得三棱锥,点M是棱BC的中点,DM=3$\sqrt{2}$.
如图,菱形ABCD的边长为6,∠BAD=60°,AC∩BD=O,将菱形ABCD沿对角线AC折起得三棱锥,点M是棱BC的中点,DM=3$\sqrt{2}$.