若实数x.y满足$\left\{\begin{array}{l}{y≥0}\\{x-2y≥2}\\{x+y≤5}\end{array}\right.$.则x+2y的最小值是2．题目和参考答案——青夏教育精英家教网—

题目内容

20．若实数x、y满足$\left\{\begin{array}{l}{y≥0}\\{x-2y≥2}\\{x+y≤5}\end{array}\right.$，则x+2y的最小值是2．

分析先画出线性约束条件表示的可行域，再将目标函数赋予几何意义，即可求出z=x+2y的最小值．

解答解：依题意作出实数x、y满足$\left\{\begin{array}{l}{y≥0}\\{x-2y≥2}\\{x+y≤5}\end{array}\right.$的可行性区域，
标函数z=x+2y可看做斜率为-$\frac{1}{2}$的动直线在y轴上的纵截距．
数形结合可知，当动直线过点A时，
目标函数值最小z=2+0=2．
故答案为：2

点评本题主要考查了线性规划的思想和方法，二元一次不等式组表示平面区域，数形结合的思想方法，属中档题．

练习册系列答案

相关题目

10．

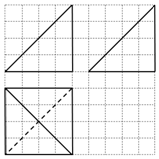某空间几何体的三视图如图所示（图中小正方形的边长为1），则这个几何体的体积是（　　）

11．设m、n是两条不同的直线，α、β为两个不同的平面，则下列为真命题的是（　　）

	A．	若m∥α，n⊥β且α⊥β，则m∥n		B．	若m⊥α，n⊥β且α⊥β，则m⊥n
	C．	若α⊥β，α∩β=m，n⊥m，则n⊥β		D．	若α∩β=m，n?α，m⊥n，则α⊥β

8．已知函数f（x）=sin（x+$\frac{π}{2}$），g（x）=cos（x+π），则下列结论中正确的是（　　）

	A．	将f（x）的图象向左平移$\frac{π}{2}$个单位后得到g（x）的图象
	B．	函数y=f（x）•g（x）的最小正周期为2π
	C．	函数y=f（x）•g（x）的最大值为1
	D．	x=$\frac{π}{2}$是函数y=f（x）•g（x）图象的一条对称轴