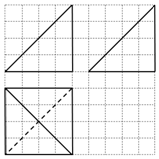某空间几何体的三视图如图所示(图中小正方形的边长为1).则这个几何体的体积是( )A．16B．32C．$\frac{64}{3}$D．$\frac{32}{3}$ 题目和参考答案——青夏教育精英家教网—

题目内容

10．

某空间几何体的三视图如图所示（图中小正方形的边长为1），则这个几何体的体积是（　　）

A．

B．

C．

$\frac{64}{3}$

D．

$\frac{32}{3}$

分析由三视图可知：该几何体为三棱锥P-ABC，过点P作PO⊥底面ABC，垂足为O，连接OB，OC，则四边形OBAC是边长为4的正方形，高PO=4．

解答解：由三视图可知：该几何体为三棱锥P-ABC，过点P作PO⊥底面ABC，垂足为O，连接OB，OC，则四边形OBAC是边长为4的正方形，高PO=4．
则该几何体的体积V=$\frac{1}{3}×\frac{1}{2}×{4}^{2}×4$=$\frac{32}{3}$．
故选：D．

点评本题考查了三棱锥的三视图、体积计算公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案

相关题目

20．若$\frac{1+mi}{1-i}$为纯虚数，则m的值为（　　）

1．如图，在矩形ABCD中，已知AB=2，AD=4，点E、F分别在AD、BC上，且AE=1，BF=3，将四边形AEFB沿EF折起，使点B在平面CDEF上的射影H在直线DE上．

（I）求证：CD⊥BE；
（II）求点B到平面CDE的距离；
（III）求直线AF与平面EFCD所成的正弦值．

18．已知$\overrightarrow a=（1，0）{，_{\;}}\overrightarrow b=（2，1）$，则$\overrightarrow a$•$\overrightarrow b$=2．

5．

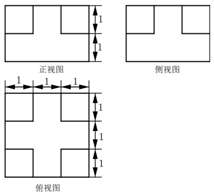榫卯（sǔn mǎo）是古代中国建筑、家具及其它器械的主要结构方式，是在两个构件上采用凹凸部位相结合的一种连接方式，凸出部分叫做“榫头”．某“榫头”的三视图及其部分尺寸如图所示，则该“榫头”体积等于（　　）

15．已知${（1+x）^{10}}={a_0}+{a_1}（1-x）+{a_2}{（1-x）^2}+…+{a_{10}}{（1-x）^{10}}$，则a₀+a₈=（　　）

2．已知平面直角坐标系xOy中，过点P（-1，-2）的直线l的参数方程为$\left\{{\begin{array}{l}{x=-1+tcos{{45}°}}\\{y=-2+tsin{{45}°}}\end{array}}\right.$（t为参数），以原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ•sinθ•tanθ=4m（m＞0），直线l与曲线C相交于不同的两点M，N．
（1）求曲线C的直角坐标方程和直线l的普通方程；
（2）若|PM|=|MN|，求实数m的值．

19．已知双曲线与椭圆x²+$\frac{{y}^{2}}{2}$=1有公共焦点，且双曲线的离心率为$\sqrt{5}$，则该双曲线的渐近线方程为（　　）

A．

y=±2x

B．

y=±$\frac{2\sqrt{5}}{5}$

C．

y=±$\frac{\sqrt{5}}{2}$x

D．

y=±$\frac{1}{2}$x

20．若实数x、y满足$\left\{\begin{array}{l}{y≥0}\\{x-2y≥2}\\{x+y≤5}\end{array}\right.$，则x+2y的最小值是2．

试题分类