题目内容
11.设m、n是两条不同的直线,α、β为两个不同的平面,则下列为真命题的是( )| A. | 若m∥α,n⊥β且α⊥β,则m∥n | B. | 若m⊥α,n⊥β且α⊥β,则m⊥n | ||
| C. | 若α⊥β,α∩β=m,n⊥m,则n⊥β | D. | 若α∩β=m,n?α,m⊥n,则α⊥β |
分析 在A中,m与n相交、平行或异面;在B中,由面面垂直及线面垂直的性质定理得m⊥n;在C中,n与β相交、平行或n?β;在D中,α与β相交或平行.
解答 解:由m、n是两条不同的直线,α、β为两个不同的平面,知:
在A中,若m∥α,n⊥β且α⊥β,则m与n相交、平行或异面,故A错误;
在B中,若m⊥α,n⊥β且α⊥β,则由面面垂直及线面垂直的性质定理得m⊥n,故B正确;
在C中,若α⊥β,α∩β=m,n⊥m,则n与β相交、平行或n?β,故C错误;
在D中,若α∩β=m,n?α,m⊥n,则α与β相交或平行,故D错误.
故选:B.
点评 本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查空间想象能力,考查化归与转化思想,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.已知双曲线与椭圆x2+$\frac{{y}^{2}}{2}$=1有公共焦点,且双曲线的离心率为$\sqrt{5}$,则该双曲线的渐近线方程为( )
| A. | y=±2x | B. | y=±$\frac{2\sqrt{5}}{5}$ | C. | y=±$\frac{\sqrt{5}}{2}$x | D. | y=±$\frac{1}{2}$x |
1.“平面α内的两条直线与平面β都平行”是“平面α与平面β平行”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
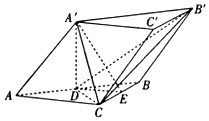 在斜三棱柱ABC-A′B′C′中,AC=BC=A′A=A′C,A′在底面ABC上的射影为AB的中点D,E为线段BC的中点.
在斜三棱柱ABC-A′B′C′中,AC=BC=A′A=A′C,A′在底面ABC上的射影为AB的中点D,E为线段BC的中点.