题目内容
在自行车比赛中，运动员的位移与比赛时间t存在关系s（t）=10t+5t2（s的单位是m，t的单位是s）．
（1）求t=20，△t=0.1时的△s与
；
（2）求t=20时的速度．
（1）求t=20，△t=0.1时的△s与
| △s |
| △t |
（2）求t=20时的速度．
考点：导数的运算
专题：导数的概念及应用
分析：（1）根据函数的平均变化率即可求出；
（2）根据导数的物理意义，先求导，再代入值计算即可．
（2）根据导数的物理意义，先求导，再代入值计算即可．
解答：
解：（1）△s=s（t+△t）-s（t）=10（t+△t）+5（t+△t）2-10t-5t2=△t2+10t△t+10△t=0.01+20+1=21.01
=
=210.1，
（2）v=s′（t）=10+10t，
当t=20时，v=s′（20）=10+10×20=210
| △s |
| △t |
| 21.01 |
| 0.1 |
（2）v=s′（t）=10+10t，
当t=20时，v=s′（20）=10+10×20=210
点评：本题考查了导数的变化率和导数的物理意义，属于基础题．
练习册系列答案
相关题目
设集合M={y|y=|cos2x-sin2x|，x∈R}，N={x|y=ln（1-x2）}，则M∩N=（ ）
| A、{x|-1≤x≤1} |
| B、{x|-1≤x≤0} |
| C、{x|0＜x≤1} |
| D、{x|0≤x＜1} |
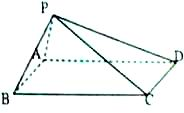如图，四棱锥P-ABCD的底面ABCD是矩形，且AB=2，BC=